
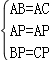
在△ABC中,如图所示,AD=AE,DB=EC,P为CD、BE的交点,则图中全等三角形的对数是( )

A.3对 B.4对 C.5 对 D.6对
对 D.6对
C【考点】全等三角形的判定.
【分析】根据等式的性质可得AB=AC,根据等边对等角可得∠ABC=∠ACB,然后再证明△DBC≌△ECB,可得CD=BE,再证明△ADC≌△AEB,可得∠1=∠2,然后再依次证明△DBP≌△ECP,△ADP≌△AEP,△ABP≌△ACP.
【解答】解:∵AD=AE,DB=EC,
∴AB=AC,
∴∠ABC=∠ACB,
在△BDC和△CEB中,
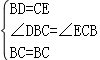 ,
,
∴△DBC≌△ECB(SAS),
∴CD=BE,
在△ADC和△AEB中,
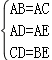 ,
,
∴△ADC≌△AEB(SSS),
∴∠1=∠2,
在△DBP和△ECP中,
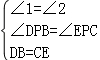 ,
,
∴△DBP≌△ECP(AAS),
∴DP=EP,PB=PC
在△ADP和△AEP中,
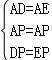 ,
,
∴△ADP≌△AEP(SSS),
在△ABP和△ACP中,
 ,
,
∴△ABP≌△ACP(SSS),
共5对.
故选:C.
【点评】本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.
注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
如图所示,在Rt△ABC中,∠A=90°,BD平分∠ABC,交AC于点D,且AB=4,BD=5,则点D到BC的距离是( )

A.3 B.4 C.5 D.6
查看答案和解析>>
科目:初中数学 来源: 题型:
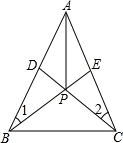
如图1,已知线段AB,CD相交于点O,连接AD,CB,我们把形如图1的图形称之为“8字形”.如图2,在图1的条件下,∠DAB和∠BCD的平分线AP和CP相交于点P,并且与CD,AB分别相交于点M,N,试解答下列问题:
(1)在图1中,请直接写出∠A、∠B、∠C、∠D之间的数量关系;
(2)在图2中,若∠D=40°,∠B=36°,试求∠P的度数;
(3)如果图2中∠D和∠B为任意角时,其他条件不变,试问∠P与∠D、∠B之间存在着怎样的数量关系(直接写出结论即可)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com