
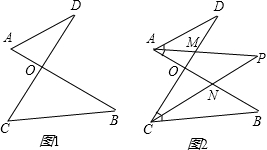
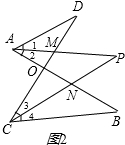
如图1,已知线段AB,CD相交于点O,连接AD,CB,我们把形如图1的图形称之为“8字形”.如图2,在图1的条件下,∠DAB和∠BCD的平分线AP和CP相交于点P,并且与CD,AB分别相交于点M,N,试解答下列问题:
(1)在图1中,请直接写出∠A、∠B、∠C、∠D之间的数量关系;
(2)在图2中,若∠D=40°,∠B=36°,试求∠P的度数;
(3)如果图2中∠D和∠B为任意角时,其他条件不变,试问∠P与∠D、∠B之间存在着怎样的数量关系(直接写出结论即可)
【考点】三角形内角和定理;三角形的外角性质.
【分析】(1)利用三角形的内角和定理表示出∠AOD与∠BOC,再根据对顶角相等可得∠AOD=∠BOC,然后整理即可得解;
(2)根据(1)的关系式求出∠OCB﹣∠OAD,再根据角平分线的定义求出∠DAM﹣∠PCM,然后利用“8字形”的关系式列式整理即可得解;
(3)根据“8字形”用∠B、∠D表示出∠OCB﹣∠OAD,再用∠D、∠P表示出∠DAM﹣∠PCM,然后根据角平分线的定义可得∠DAM﹣∠PCM=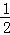 (∠OCB﹣∠OAD),然后整理即可得证.
(∠OCB﹣∠OAD),然后整理即可得证.
【解答】解:(1)在△AOD中,∠AOD=180°﹣∠A﹣∠D,
在△BOC中,∠BOC=180°﹣∠B﹣∠C,
∵∠AOD=∠BOC(对顶角相等),
∴180°﹣∠A﹣∠D=180°﹣∠B﹣∠C,
∴∠A+∠D=∠B+∠C;
(2)∵∠D=40°,∠B=36°,
∴∠OAD+40°=∠OCB+36°,
∴∠OCB﹣∠OAD=4°,
∵AP、CP分别是∠DAB和∠BCD的角平分线,
∴∠DAM=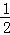 ∠OAD,∠PCM=
∠OAD,∠PCM=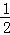 ∠OCB,
∠OCB,
又∵∠DAM+∠D=∠PCM+∠P,
∴∠P=∠DAM+∠D﹣∠PCM=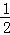 (∠OAD﹣∠OCB)+∠D=
(∠OAD﹣∠OCB)+∠D=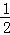 ×(﹣4°)+40°=38°;
×(﹣4°)+40°=38°;
(3)根据“8字形”数量关系,∠OAD+∠D=∠OCB+∠B,∠DAM+∠D=∠PCM+∠P,
所以,∠OCB﹣∠OAD=∠D﹣∠B,∠PCM﹣∠DAM=∠D﹣∠P,
∵AP、CP分别是∠DAB和∠BCD的角平分线,
∴∠DAM=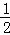 ∠OAD,∠PCM=
∠OAD,∠PCM=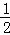 ∠OCB,
∠OCB,
∴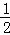 (∠D﹣∠B)=∠D﹣∠P,
(∠D﹣∠B)=∠D﹣∠P,
整 理得,2∠P=∠B+∠D.
理得,2∠P=∠B+∠D.
【点评】本题考查了三角形内角和定理,角平分线的定义,多边形的内角和定理,对顶角相等的性质,整体思想的利用是解题的关键.


科目:初中数学 来源: 题型:
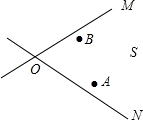
如图,学校要在两条小路OM和ON之间的S区域规划修建一处“英语角”,按照设计要求,英语角C到两栋教学楼A,B的距离必须相等,到两条小路的距离也必须相等,则“英语角”应修建在什么位置?请在图上标出它的位置.(尺规作图,保留痕迹)
查看答案和解析>>
科目:初中数学 来源: 题型:
⊙O为△ABC的外接圆,请仅用无刻度的直尺,根据下列条件分别在图1,图2中画出一条弦,使这条弦将△ABC分成面积相等的两部分(保留作图痕迹,不写作法).
(1)如图1,AC=BC;
(2)如图2,直线l与⊙O相切于点P,且l∥BC.


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com