
【题目】如图,在△ABC中,∠BAC=90°,AD是高,BE是中线,CF是角平分线,CF交AD于点G,交BE于点H,下面说法中正确的序号是_____.
①△ABE的面积等于△BCE的面积;②∠AFG=∠AGF;③∠FAG=2∠ACF;④BH=CH.

【答案】①②③
【解析】
根据等底等高的三角形的面积相等即可判断①;根据三角形内角和定理求出∠ABC=∠CAD,根据三角形的外角性质即可推出②;根据三角形内角和定理求出∠FAG=∠ACD,根据角平分线定义即可判断③;根据等腰三角形的判定判断④即可.
解:∵BE是中线,
∴AE=CE,
∴△ABE的面积=△BCE的面积(等底等高的三角形的面积相等),故①正确;
∵CF是角平分线,
∴∠ACF=∠BCF,
∵AD为高,
∴∠ADC=90°,
∵∠BAC=90°,
∴∠ABC+∠ACB=90°,∠ACB+∠CAD=90°,
∴∠ABC=∠CAD,
∵∠AFG=∠ABC+∠BCF,∠AGF=∠CAD+∠ACF,
∴∠AFG=∠AGF,故②正确;
∵AD为高,
∴∠ADB=90°,
∵∠BAC=90°,
∴∠ABC+∠ACB=90°,∠ABC+∠BAD=90°,
∴∠ACB=∠BAD,
∵CF是∠ACB的平分线,
∴∠ACB=2∠ACF,
∴∠BAD=2∠ACF,
即∠FAG=2∠ACF,故③正确;
根据已知条件不能推出∠HBC=∠HCB,即不能推出BH=CH,故④错误;
故答案为:①②③.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】等边三角形ABC的边长为6,在AC,BC边上各取一点E,F,连接AF,BE相交于点P. 
(1)若AE=CF; ①求证:AF=BE,并求∠APB的度数;
②若AE=2,试求APAF的值;
(2)若AF=BE,当点E从点A运动到点C时,试求点P经过的路径长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y1=﹣2x2+2,直线y2=2x+2,当x任取一值时,x对应的函数值分别为y1、y2 . 若y1≠y2 , 取y1、y2中的较小值记为M;若y1=y2 , 记M=y1=y2 . 例如:当x=1时,y1=0,y2=4,y1<y2 , 此时M=0.下列判断:
①当x>0时,y1>y2;
②当x<0时,x值越大,M值越小;
③使得M大于2的x值不存在;
④使得M=1的x值是﹣ ![]() 或
或 ![]() .
.
其中正确的是( )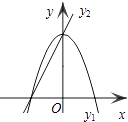
A.①②
B.①④
C.②③
D.③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两辆货车分别从![]() 、
、![]() 两地出发,沿同一条公路相向而行,当到达对方的出发地后立即装卸货物,5分钟后再按原路以原速度返回各自的出发地,已知
两地出发,沿同一条公路相向而行,当到达对方的出发地后立即装卸货物,5分钟后再按原路以原速度返回各自的出发地,已知![]() 、
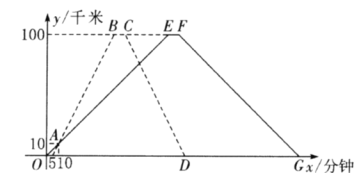
、![]() 两地相距100千米.甲车比乙车早5分钟出发,甲车出发10分钟时两车都行驶了10千米,甲、乙两车离各自出发地的路程
两地相距100千米.甲车比乙车早5分钟出发,甲车出发10分钟时两车都行驶了10千米,甲、乙两车离各自出发地的路程![]() (千米)与甲车出发时间
(千米)与甲车出发时间![]() (分钟)的函数图像如图所示.
(分钟)的函数图像如图所示.
(1)甲车从![]() 地出发后,经过多长时间甲、乙两车第一次相遇?
地出发后,经过多长时间甲、乙两车第一次相遇?
(2)乙车从![]() 地出发后,经过多长时间甲、乙两车与各自出发地的距离相等?
地出发后,经过多长时间甲、乙两车与各自出发地的距离相等?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,E为AC的中点,AD平分∠BAC,BA:CA=2:3,AD与BE相交于点O,若△OAE的面积比△BOD的面积大1,则△ABC的面积是( )

A. 8 B. 9 C. 10 D. 11
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一渔船由西往东航行,在A点测得海岛C位于北偏东60°的方向,前进20海里到达B点,此时,测得海岛C位于北偏东30°的方向,则海岛C到航线AB的距离CD等于海里.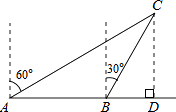
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为1的正方形组成的网格中,△AOB的顶点均在格点上,点A、B的坐标分别是A(3,2),B(1,3),△AOB绕点O逆时针旋转90°后得到△A1OB1 . 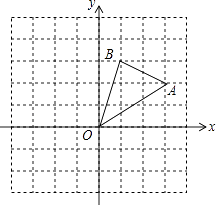
(1)点A关于点O中心对称的点P的坐标为;
(2)在网格内画出△A1OB1;
(3)点A1、B1的坐标分别为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形OABC的顶点A,C分别在x轴和y轴上,点B的坐标为(4,6).双曲线y= ![]() (x>0)的图象经过BC的中点D,且与AB交于点E,连接DE.
(x>0)的图象经过BC的中点D,且与AB交于点E,连接DE.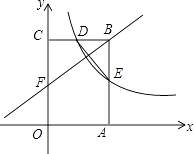
(1)求k的值及点E的坐标;
(2)若点F是边上一点,且△BCF∽△EBD,求直线FB的解析式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com