
【题目】如图,矩形OABC的顶点A,C分别在x轴和y轴上,点B的坐标为(4,6).双曲线y= ![]() (x>0)的图象经过BC的中点D,且与AB交于点E,连接DE.
(x>0)的图象经过BC的中点D,且与AB交于点E,连接DE.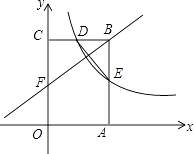
(1)求k的值及点E的坐标;
(2)若点F是边上一点,且△BCF∽△EBD,求直线FB的解析式.
【答案】
(1)
解:在矩形OABC中,
∵B(4,6),
∴BC边中点D的坐标为(2,6),
∵又曲线y= ![]() 的图象经过点(2,6),
的图象经过点(2,6),
∴k=12,
∵E点在AB上,
∴E点的横坐标为4,
∵y= ![]() 经过点E,
经过点E,
∴E点纵坐标为3,
∴E点坐标为(4,3)
(2)
解:由(1)得,BD=2,BE=3,BC=4,
∵△FBC∽△DEB,
∴ ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,
,
∴CF= ![]() ,
,
∴OF= ![]() ,即点F的坐标为(0,
,即点F的坐标为(0, ![]() ),
),
设直线FB的解析式为y=kx+b,而直线FB经过B(4,6),F(0, ![]() ),
),
∴ 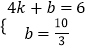 ,解得
,解得 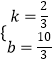 ,
,
∴直线BF的解析式为y= ![]() x+
x+ ![]()
【解析】(1)由条件可先求得点D的坐标,代入反比例函数可求得k的值,又由点E的位置可求得E点的横坐标,代入可求得E点坐标;(2)由相似三角形的性质可求得CF的长,可求得OF,则可求得F点的坐标,利用待定系数法可求得直线FB的解析式.
【考点精析】本题主要考查了反比例函数的图象和反比例函数的性质的相关知识点,需要掌握反比例函数的图像属于双曲线.反比例函数的图象既是轴对称图形又是中心对称图形.有两条对称轴:直线y=x和 y=-x.对称中心是:原点;性质:当k>0时双曲线的两支分别位于第一、第三象限,在每个象限内y值随x值的增大而减小; 当k<0时双曲线的两支分别位于第二、第四象限,在每个象限内y值随x值的增大而增大才能正确解答此题.


科目:初中数学 来源: 题型:
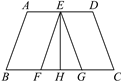
【题目】如图所示,已知AD∥BC,AB∥EF,CD∥EG,且点E在直线AD上,点F,H,G在直线BC上,EH平分∠FEG,∠A=∠D=110°,线段EH的长是不是两条平行线AD,BC之间的距离?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠BAC=90°,AD是高,BE是中线,CF是角平分线,CF交AD于点G,交BE于点H,下面说法中正确的序号是_____.
①△ABE的面积等于△BCE的面积;②∠AFG=∠AGF;③∠FAG=2∠ACF;④BH=CH.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E正方形ABCD外一点,点F是线段AE上一点,△EBF是等腰直角三角形,其中∠EBF=90°,连接CE、CF.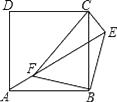
(1)求证:△ABF≌△CBE;
(2)判断△CEF的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:
小明在学习二次根式的化简后,遇到了这样一个需要化简的式子:![]() .该如何化简呢?思考后,他发现3+2
.该如何化简呢?思考后,他发现3+2![]() =1+2
=1+2![]() +(
+(![]() )2=(1+
)2=(1+![]() )2.于是
)2.于是![]() =
=![]() =1+
=1+![]() .善于思考的小明继续深入探索;当a+b
.善于思考的小明继续深入探索;当a+b![]() =(m+n
=(m+n![]() )2时(其中a,b,m,n均为正整数),则a+b
)2时(其中a,b,m,n均为正整数),则a+b![]() =m2+2
=m2+2![]() mn+2n2.此时,a=m2+2n2,b=2mn,于是,
mn+2n2.此时,a=m2+2n2,b=2mn,于是,![]() =m+n
=m+n![]() .请你仿照小明的方法探索并解决下列问题:
.请你仿照小明的方法探索并解决下列问题:
(1)设a,b,m,n均为正整数且![]() =m+n
=m+n![]() ,用含m,n的式子分别表示a,b时,结果是a= ,b= ;
,用含m,n的式子分别表示a,b时,结果是a= ,b= ;
(2)利用(1)中的结论,选择一组正整数填空:![]() = +
= + ![]() ;
;
(3)化简:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算
(1)﹣18×(﹣2)÷3
(2)(﹣![]() )×(﹣90)÷
)×(﹣90)÷![]()
(3)﹣2.5÷![]() ×(﹣
×(﹣![]() );
);
(4)(﹣10)2﹣[16+(﹣3)2]
(5)(![]() ﹣
﹣![]() +2)÷
+2)÷![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=ax2﹣2x与x轴正半轴相交于点A,顶点为B.
(1)用含a的式子表示点B的坐标;
(2)经过点C(0,﹣2)的直线AC与OB(O为原点)相交于点D,与抛物线的对称轴相交于点E,△OCD≌△BED,求a的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com