【题目】如图，点E正方形ABCD外一点，点F是线段AE上一点，△EBF是等腰直角三角形，其中∠EBF=90°，连接CE、CF．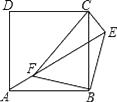
（1）求证：△ABF≌△CBE；
（2）判断△CEF的形状，并说明理由．
【答案】
（1）
证明：∵四边形ABCD是正方形，
∴AB=CB，∠ABC=90°，
∵△EBF是等腰直角三角形，其中∠EBF=90°，
∴BE=BF，
∴∠ABC﹣∠CBF=∠EBF﹣∠CBF，
∴∠ABF=∠CBE．
在△ABF和△CBE中，有 
，
∴△ABF≌△CBE（SAS）．
（2）
解：△CEF是直角三角形．理由如下：
∵△EBF是等腰直角三角形，
∴∠BFE=∠FEB=45°，
∴∠AFB=180°﹣∠BFE=135°，
又∵△ABF≌△CBE，
∴∠CEB=∠AFB=135°，
∴∠CEF=∠CEB﹣∠FEB=135°﹣45°=90°，
∴△CEF是直角三角形．
【解析】（1）根据正方形的性质，得到AB=CB，∠ABC=90度，从而可转成∠ABF=∠EBC，则根据“SAS”判定全等；
（2）根据等腰直角三角形，和全等三角形的性质去解答.
科目：初中数学 来源： 题型：
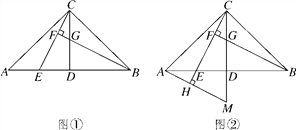
【题目】如图，在△ABC中，AC＝BC，∠ACB＝90°，D是AB的中点，点E是AB边上一点．
（1）BF⊥CE于点F，交CD于点G(如图①)．求证：AE＝CG；
（2）AH⊥CE，垂足为H，交CD的延长线于点M(如图②)，找出图中与BE相等的线段，并证明．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在△ABC中，E为AC的中点，AD平分∠BAC，BA：CA=2：3，AD与BE相交于点O，若△OAE的面积比△BOD的面积大1，则△ABC的面积是（ ）
A. 8 B. 9 C. 10 D. 11
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在边长为1的正方形组成的网格中，△AOB的顶点均在格点上，点A、B的坐标分别是A（3，2），B（1，3），△AOB绕点O逆时针旋转90°后得到△A1OB1 ．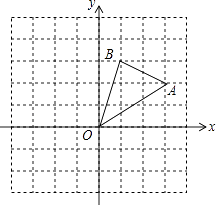 
（1）点A关于点O中心对称的点P的坐标为；
（2）在网格内画出△A1OB1；
（3）点A1、B1的坐标分别为 ．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，直线m，n的夹角为35°，相交于点O．
（1）作出△ABC关于直线m的对称△DEF；
（2）作出△DEF关于直线n的对称△PQR；
（3）△PQR还可以由△ABC经过一次怎样的变换得到．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，矩形OABC的顶点A，C分别在x轴和y轴上，点B的坐标为（4，6）．双曲线y= 
（x＞0）的图象经过BC的中点D，且与AB交于点E，连接DE．
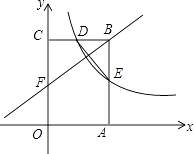
（1）求k的值及点E的坐标；
（2）若点F是边上一点，且△BCF∽△EBD，求直线FB的解析式．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在矩形OABC中，点A在x轴的正半轴，点C在y轴的正半轴．抛物线y= 
x2﹣ 
x+4经过点B，C，连接OB，D是OB上的动点，过D作DE∥OA交抛物线于点E（在对称轴右侧），过E作EF⊥OB于F，以ED，EF为邻边构造DEFG，则DEFG周长的最大值为 ． 
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，⊙O是以AB为直径的圆，C为⊙O上一点，AE和过点C的切线互相垂直，垂足为E，AE交⊙O于点D，直线EC交AB的延长线于点F，连结CA，CB． 
（1）求证：AC平分∠DAB；
（2）若⊙O的半径为5，且tan∠DAC= 
，求BC的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，一个长方体的表面展开图中四边形ABCD是正方形(正方形的四个角都是直角、四条边都相等)，则根据图中数据可得原长方体的体积是_________cm3．
【答案】20
【解析】
利用正方形的性质以及图形中标注的长度得出AB=AE=5cm，进而得出长方体的长、宽、高进而得出答案．
如图：
，
∵四边形ABCD是正方形，
∴AB=AE=5cm，
∴立方体的高为：（7-5）÷2=1（cm），
∴EF=5-1=4（cm），
∴原长方体的体积是：5×4×1=20（cm3）．
故答案为：20．
【点睛】
此题主要考查了几何体的展开图，利用已知图形得出各边长是解题关键．
【题型】填空题
【结束】
19
【题目】计算：
（1）-4-28-(-19)+(-24)；
（2）-14÷(2017-π)0-(-
)-2.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com