
【题目】如图,在矩形OABC中,点A在x轴的正半轴,点C在y轴的正半轴.抛物线y= ![]() x2﹣
x2﹣ ![]() x+4经过点B,C,连接OB,D是OB上的动点,过D作DE∥OA交抛物线于点E(在对称轴右侧),过E作EF⊥OB于F,以ED,EF为邻边构造DEFG,则DEFG周长的最大值为 .
x+4经过点B,C,连接OB,D是OB上的动点,过D作DE∥OA交抛物线于点E(在对称轴右侧),过E作EF⊥OB于F,以ED,EF为邻边构造DEFG,则DEFG周长的最大值为 . 
【答案】![]()
【解析】解:当x=0时,y= ![]() x2﹣
x2﹣ ![]() x+4=4, ∴点C(0,4);
x+4=4, ∴点C(0,4);
∵y= ![]() x2﹣
x2﹣ ![]() x+4=4
x+4=4 ![]() ,
,
∴抛物线的对称轴为x= ![]() ,
,
∵四边形OABC为矩形,
∴B(3,4).
设直线OB的解析式为y=kx,
将B(3,4)代入y=kx中,
4=3k,解得:k= ![]() ,
,
∴直线OB的解析式为y= ![]() x.
x.
在Rt△OAB中,OA=3,AB=4,
∴OB= ![]() =5.
=5.
∵DE∥OA,
∴∠BOA=∠EDF,
∵EF⊥OB,
∴ ![]()
∴EF= ![]() DE,
DE,
∴DEFG周长=2(EF+DE)= ![]() DE.
DE.
设点D的坐标为( ![]() m,m),则点E的坐标为(
m,m),则点E的坐标为( ![]() +
+ ![]() ,m),
,m),
∴DE= ![]() +
+ ![]() ﹣
﹣ ![]() m=﹣
m=﹣ ![]() (m﹣
(m﹣ ![]() )+
)+ ![]() =﹣
=﹣ ![]() +
+ ![]() ,
,
∴当m= ![]() 时,DE取最大值
时,DE取最大值 ![]() ,此时DEFG周长取最大值
,此时DEFG周长取最大值 ![]() .
.
所以答案是 ![]() .
.
【考点精析】掌握二次函数的性质和二次函数的最值是解答本题的根本,需要知道增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小;如果自变量的取值范围是全体实数,那么函数在顶点处取得最大值(或最小值),即当x=-b/2a时,y最值=(4ac-b2)/4a.


科目:初中数学 来源: 题型:
【题目】一张圆心角为45°的扇形纸板和圆形纸板按如图方式分别剪成一个正方形,边长都为1,则扇形和圆形纸板的面积比是( ) 
A.5:4
B.5:2
C.![]() :2
:2
D.![]() :
: ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中有一个轴对称图形,A(3,-2),B(3,﹣6)两点在此图形上且互为对称点,若此图形上有一个点C(﹣2,+1).
(1)求点C的对称点的坐标.
(2)求△ABC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E正方形ABCD外一点,点F是线段AE上一点,△EBF是等腰直角三角形,其中∠EBF=90°,连接CE、CF.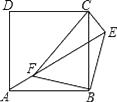
(1)求证:△ABF≌△CBE;
(2)判断△CEF的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在风速为25 km/h的条件下,一架飞机顺风从A机场飞到B机场要用5.6h,它逆风飞行同样的航线要用6h.求:
(1)无风时这架飞机在这一航线的平均航速;
(2)两机场之间的航程是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在方格纸中,点A,B,P,Q都在格点上.请按要求画出以AB为边的格点四边形.
(1)在图甲中画出一个ABCD,使得点P为ABCD的对称中心;
(2)在图乙中画出一个ABCD,使得点P,Q都在ABCD的对角线上.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学为了解学生的课外阅读情况,就“我最喜爱的课外读物”从文学、艺术、科普和其它四个类别进行了抽样调查(每位同学仅选一项),并根据调查结果制作了尚不完整的频数分布表:
类别 | 频数(人数) | 频率 |
文学 | m | 0.42 |
艺术 | 22 | 0.11 |
科普 | 66 | n |
其他 | 28 | |
合计 | 1 |
(1)表中m= , n=;
(2)在这次抽样调查中,最喜爱阅读哪类读物的学生最少?
(3)根据以上调查,试估计该校1200名学生中最喜爱阅读科普读物的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△AOB与△ACD均为正三角形,且顶点B、D均在双曲线y= ![]() (x>0)上,点A、C在x轴上,连接BC交AD于点P,则△OBP的面积= .
(x>0)上,点A、C在x轴上,连接BC交AD于点P,则△OBP的面积= . 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com