
【题目】一张圆心角为45°的扇形纸板和圆形纸板按如图方式分别剪成一个正方形,边长都为1,则扇形和圆形纸板的面积比是( ) 
A.5:4
B.5:2
C.![]() :2
:2
D.![]() :
: ![]()
【答案】A
【解析】解:如图1,连接OD, ∵四边形ABCD是正方形,
∴∠DCB=∠ABO=90°,AB=BC=CD=1,
∵∠AOB=45°,
∴OB=AB=1,
由勾股定理得:OD= ![]() =
= ![]() ,
,
∴扇形的面积是 ![]() =
= ![]() π;
π;
如图2,连接MB、MC,
∵四边形ABCD是⊙M的内接四边形,四边形ABCD是正方形,
∴∠BMC=90°,MB=MC,
∴∠MCB=∠MBC=45°,
∵BC=1,
∴MC=MB= ![]() ,
,
∴⊙M的面积是π×( ![]() )2=
)2= ![]() π,
π,
∴扇形和圆形纸板的面积比是 ![]() π÷(
π÷( ![]() π)=
π)= ![]() .
.
故选:A.
【考点精析】本题主要考查了勾股定理的概念和正多边形和圆的相关知识点,需要掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;圆的内接四边形的对角互补,并且任何一个外角都等于它的内对角;圆的外切四边形的两组对边的和相等才能正确解答此题.


科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点A、B的坐标分别是(0,3)、(﹣4,0),
(1)将△AOB绕点A逆时针旋转90°得到△AEF,点O,B对应点分别是E,F,请在图中画出△AEF,并写出E、F的坐标;
(2)以O点为位似中心,将△AEF作位似变换且缩小为原来的 ![]() ,在网格内画出一个符合条件的△A1E1F1 .
,在网格内画出一个符合条件的△A1E1F1 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A,B,C在一条直线上,△ABD,△BCE均为等边三角形,连接AE和CD,AE分别交CD,BD于点M,P,CD交BE于点Q,连接PQ,BM,下面结论:
①△ABE≌△DBC;②∠DMA=60°;③△BPQ为等边三角形;④MB平分∠AMC,
其中结论正确的有( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
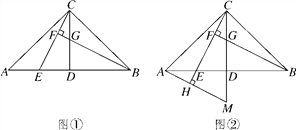
【题目】如图,在△ABC中,AC=BC,∠ACB=90°,D是AB的中点,点E是AB边上一点.
(1)BF⊥CE于点F,交CD于点G(如图①).求证:AE=CG;
(2)AH⊥CE,垂足为H,交CD的延长线于点M(如图②),找出图中与BE相等的线段,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y1=ax2+bx+c(a≠0)与x轴相交于点A,B(点A,B在原点O两侧),与y轴相交于点C,且点A,C在一次函数y2= ![]() x+n的图象上,线段AB长为16,线段OC长为8,当y1随着x的增大而减小时,求自变量x的取值范围.
x+n的图象上,线段AB长为16,线段OC长为8,当y1随着x的增大而减小时,求自变量x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y1=﹣2x2+2,直线y2=2x+2,当x任取一值时,x对应的函数值分别为y1、y2 . 若y1≠y2 , 取y1、y2中的较小值记为M;若y1=y2 , 记M=y1=y2 . 例如:当x=1时,y1=0,y2=4,y1<y2 , 此时M=0.下列判断:
①当x>0时,y1>y2;
②当x<0时,x值越大,M值越小;
③使得M大于2的x值不存在;
④使得M=1的x值是﹣ ![]() 或
或 ![]() .
.
其中正确的是( )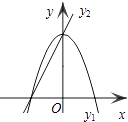
A.①②
B.①④
C.②③
D.③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在烧开水时,水温达到100℃就会沸腾,下表是某同学做“观察水的沸腾”实验时记录的数据:

(1)上表反映了哪两个量之间的关系?哪个是自变量?哪个是因变量?
(2)水的温度是如何随着时间的变化而变化的?
(3)时间推移2分钟,水的温度如何变化?
(4)时间为8分钟时,水的温度为多少?你能得出时间为9分钟时,水的温度吗?
(5)根据表格,你认为时间为16分钟和18分钟时水的温度分别为多少?
(6)为了节约能源,你认为应在什么时间停止烧水?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,E为AC的中点,AD平分∠BAC,BA:CA=2:3,AD与BE相交于点O,若△OAE的面积比△BOD的面积大1,则△ABC的面积是( )

A. 8 B. 9 C. 10 D. 11
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形OABC中,点A在x轴的正半轴,点C在y轴的正半轴.抛物线y= ![]() x2﹣
x2﹣ ![]() x+4经过点B,C,连接OB,D是OB上的动点,过D作DE∥OA交抛物线于点E(在对称轴右侧),过E作EF⊥OB于F,以ED,EF为邻边构造DEFG,则DEFG周长的最大值为 .
x+4经过点B,C,连接OB,D是OB上的动点,过D作DE∥OA交抛物线于点E(在对称轴右侧),过E作EF⊥OB于F,以ED,EF为邻边构造DEFG,则DEFG周长的最大值为 . 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com