
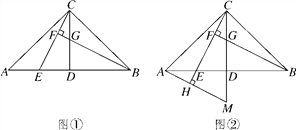
【题目】如图,在△ABC中,AC=BC,∠ACB=90°,D是AB的中点,点E是AB边上一点.
(1)BF⊥CE于点F,交CD于点G(如图①).求证:AE=CG;
(2)AH⊥CE,垂足为H,交CD的延长线于点M(如图②),找出图中与BE相等的线段,并证明.
【答案】(1)证明见解析(2)BE=CM.证明见解析.
【解析】试题分析:(1)首先根据点D是AB中点,∠ACB=90°,可得出∠ACD=∠BCD=45°,判断出△AEC≌△CGB,即可得出AE=CG,
(2)根据垂直的定义得出∠CMA+∠MCH=90°,∠BEC+∠MCH=90°,再根据AC=BC,∠ACM=∠CBE=45°,得出△BCE≌△CAM,进而证明出BE=CM.
(1)证明:∵点D是AB中点,AC=BC,
∠ACB=90°,
∴CD⊥AB,∠ACD=∠BCD=45°,
∴∠CAD=∠CBD=45°,
∴∠CAE=∠BCG,
又∵BF⊥CE,
∴∠CBG+∠BCF=90°,
又∵∠ACE+∠BCF=90°,
∴∠ACE=∠CBG,
在△AEC和△CGB中,
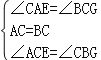
∴△AEC≌△CGB(ASA),
∴AE=CG,
(2)解:BE=CM.
证明:∵CH⊥HM,CD⊥ED,
∴∠CMA+∠MCH=90°,∠BEC+∠MCH=90°,
∴∠CMA=∠BEC,
又∵∠ACM=∠CBE=45°,
在△BCE和△CAM中, ,
,
∴△BCE≌△CAM(AAS),
∴BE=CM.


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠B=40°,∠C=60°,AD⊥BC于D,AE是∠BAC的平分线.

(1)求∠DAE的度数;
(2)写出以AD为高的所有三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
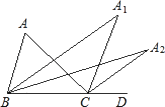
【题目】如图△ABC中,∠A=96°,延长BC到D,∠ABC与∠ACD的平分线相交于点A1∠A1BC与∠A1CD的平分线相交于点A2,依此类推,∠A4BC与∠A4CD的平分线相交于点A5,则∠A5的度数为( )
A. 19.2° B. 8° C. 6° D. 3°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小苏和小林在如图所示的跑道上进行4×50米折返跑.在整个过程中,跑步者距起跑线的距离y(单位:m)与跑步时间t(单位:s)的对应关系如下图所示.下列叙述正确的是( )

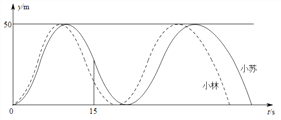
A. 两人从起跑线同时出发,同时到达终点
B. 小苏跑全程的平均速度大于小林跑全程的平均速度
C. 小苏前15s跑过的路程大于小林前15s跑过的路程
D. 小林在跑最后100m的过程中,与小苏相遇2次
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】给出下列命题及函数y=x,y=x2和y= ![]() 的图象:
的图象:
①如果 ![]() ,那么0<a<1;
,那么0<a<1;
②如果 ![]() ,那么a>1;
,那么a>1;
③如果 ![]() ,那么﹣1<a<0;
,那么﹣1<a<0;
④如果 ![]() 时,那么a<﹣1.
时,那么a<﹣1.
则( )
A.正确的命题是①④
B.错误的命题是②③④
C.正确的命题是①②
D.错误的命题只有③
查看答案和解析>>
科目:初中数学 来源: 题型:
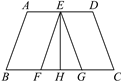
【题目】如图所示,已知AD∥BC,AB∥EF,CD∥EG,且点E在直线AD上,点F,H,G在直线BC上,EH平分∠FEG,∠A=∠D=110°,线段EH的长是不是两条平行线AD,BC之间的距离?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一张圆心角为45°的扇形纸板和圆形纸板按如图方式分别剪成一个正方形,边长都为1,则扇形和圆形纸板的面积比是( ) 
A.5:4
B.5:2
C.![]() :2
:2
D.![]() :
: ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2012义乌市)在锐角△ABC中,AB=4,BC=5,∠ACB=45°,将△ABC绕点B按逆时针方向旋转,得到△A1BC1 . 
(1)如图1,当点C1在线段CA的延长线上时,求∠CC1A1的度数;
(2)如图2,连接AA1 , CC1 . 若△ABA1的面积为4,求△CBC1的面积;
(3)如图3,点E为线段AB中点,点P是线段AC上的动点,在△ABC绕点B按逆时针方向旋转过程中,点P的对应点是点P1 , 求线段EP1长度的最大值与最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E正方形ABCD外一点,点F是线段AE上一点,△EBF是等腰直角三角形,其中∠EBF=90°,连接CE、CF.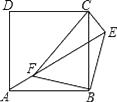
(1)求证:△ABF≌△CBE;
(2)判断△CEF的形状,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com