【题目】如图，点A，B，C在一条直线上，△ABD，△BCE均为等边三角形，连接AE和CD，AE分别交CD，BD于点M，P，CD交BE于点Q，连接PQ，BM，下面结论：

①△ABE≌△DBC；②∠DMA=60°；③△BPQ为等边三角形；④MB平分∠AMC，

其中结论正确的有（ ）

A. 1个 B. 2个 C. 3个 D. 4个

参考答案：

【答案】D

【解析】试题分析：∵△ABD、△BCE为等边三角形，

∴AB=DB，∠ABD=∠CBE=60°，BE=BC，

∴∠ABE=∠DBC，∠PBQ=60°，

在△ABE和△DBC中，，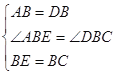

∴△ABE≌△DBC（SAS），

∴①正确；

∵△ABE≌△DBC，

∴∠BAE=∠BDC，

∵∠BDC+∠BCD=180°﹣60°﹣60°=60°，

∴∠DMA=∠BAE+∠BCD=∠BDC+∠BCD=60°，

∴②正确；

在△ABP和△DBQ中，，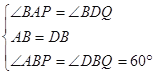

∴△ABP≌△DBQ（ASA），∴BP=BQ，∴△BPQ为等边三角形，

∴③正确；∵∠DMA=60°，∴∠AMC=120°，∴∠AMC+∠PBQ=180°，

∴P、B、Q、M四点共圆，∵BP=BQ，∴，∴∠BMP=∠BMQ，

即MB平分∠AMC；∴④正确；

综上所述：正确的结论有4个；

故选：D．

关闭