
【题目】如图,⊙O是以AB为直径的圆,C为⊙O上一点,AE和过点C的切线互相垂直,垂足为E,AE交⊙O于点D,直线EC交AB的延长线于点F,连结CA,CB. 
(1)求证:AC平分∠DAB;
(2)若⊙O的半径为5,且tan∠DAC= ![]() ,求BC的长.
,求BC的长.
【答案】
(1)证明:∵EF为切线,
∴OC⊥EF,
∵AE⊥EF,
∴AE∥OC,
∴∠EAC=∠OCA,
∵OA=OC,
∴∠OCA=∠OAC,
∴∠OAC=∠OCA,
∴AC平分∠DAB;
(2)解:∵∠OAC=∠OCA,
∴tan∠OAC=tan∠DAC= ![]() ,
,
设BC=x,则AC=2x,
∴AB= ![]() x,
x,
∴ ![]() x=10,解得x=2
x=10,解得x=2 ![]() ,
,
∴BC=2 ![]() .
.
【解析】(1)利用切线的性质得到OC⊥EF,而AE⊥EF,则可判定AE∥OC,利用平行线的性质得到∠EAC=∠OCA,加上∠OCA=∠OAC,于是得到∠OAC=∠OCA;(2)利用∠OAC=∠OCA得到tan∠OAC=tan∠DAC= ![]() ,设BC=x,则AC=2x,根据勾股定理得到AB=
,设BC=x,则AC=2x,根据勾股定理得到AB= ![]() x,则
x,则 ![]() x=10,然后解方程求出x即可得到BC的长.
x=10,然后解方程求出x即可得到BC的长.


科目:初中数学 来源: 题型:
【题目】2012义乌市)在锐角△ABC中,AB=4,BC=5,∠ACB=45°,将△ABC绕点B按逆时针方向旋转,得到△A1BC1 . 
(1)如图1,当点C1在线段CA的延长线上时,求∠CC1A1的度数;
(2)如图2,连接AA1 , CC1 . 若△ABA1的面积为4,求△CBC1的面积;
(3)如图3,点E为线段AB中点,点P是线段AC上的动点,在△ABC绕点B按逆时针方向旋转过程中,点P的对应点是点P1 , 求线段EP1长度的最大值与最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E正方形ABCD外一点,点F是线段AE上一点,△EBF是等腰直角三角形,其中∠EBF=90°,连接CE、CF.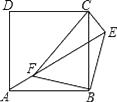
(1)求证:△ABF≌△CBE;
(2)判断△CEF的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在方格纸中,点A,B,P,Q都在格点上.请按要求画出以AB为边的格点四边形.
(1)在图甲中画出一个ABCD,使得点P为ABCD的对称中心;
(2)在图乙中画出一个ABCD,使得点P,Q都在ABCD的对角线上.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算
(1)﹣18×(﹣2)÷3
(2)(﹣![]() )×(﹣90)÷
)×(﹣90)÷![]()
(3)﹣2.5÷![]() ×(﹣
×(﹣![]() );
);
(4)(﹣10)2﹣[16+(﹣3)2]
(5)(![]() ﹣
﹣![]() +2)÷
+2)÷![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学为了解学生的课外阅读情况,就“我最喜爱的课外读物”从文学、艺术、科普和其它四个类别进行了抽样调查(每位同学仅选一项),并根据调查结果制作了尚不完整的频数分布表:
类别 | 频数(人数) | 频率 |
文学 | m | 0.42 |
艺术 | 22 | 0.11 |
科普 | 66 | n |
其他 | 28 | |
合计 | 1 |
(1)表中m= , n=;
(2)在这次抽样调查中,最喜爱阅读哪类读物的学生最少?
(3)根据以上调查,试估计该校1200名学生中最喜爱阅读科普读物的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】东东想把一根70 cm长的木棒放到一个长、宽、高分别为30 cm,40 cm,50 cm的木箱中,他能放进去吗?答:______. (填“能”或“不能”)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com