
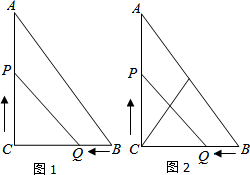
���� ��1���ֱ��ʾ���߶�PC���߶�CQ�ij�������S��PCQ=$\frac{1}{3}$S��ABC�г�������⣻
��2�����˶�ʱ��Ϊts����PCQ���ACB���ƣ�����PCQ���ACB����ʱ����֪��CPQ=��A���CPQ=��B������$\frac{CP}{CA}$=$\frac{CQ}{CB}$��$\frac{CP}{CB}$=$\frac{CQ}{CA}$���ֱ����ɵõ�����t�ķ��̣������t��ֵ��
��3�����˶�ʱ��Ϊys��PQ��CD���ഹֱ������ֱ��������б���ϵ����ߵ������Լ����������ε����ʵó���ACD=��A����BCD=��B����֤����PCQ�ס�BCA����ô$\frac{PC}{BC}$=$\frac{CQ}{AC}$�������г�����ʽ$\frac{2y}{6}$=$\frac{6-y}{8}$���ⷽ�̼��ɣ�
��� �⣺��1���辭��x���PCQ�����Ϊ��ACB�������$\frac{1}{3}$��
������ã�PC=2xm��CQ=��6-x��m��
��$\frac{1}{2}$��2x��6-x��=$\frac{1}{3}$��$\frac{1}{2}$��8��6��
��ã�x=2��x=4��
�ʾ���2���4�룬��PCQ�����Ϊ��ACB�������$\frac{1}{3}$��
��2�����˶�ʱ��Ϊts����PCQ���ACB���ƣ�
����PCQ���ACB����ʱ������$\frac{CP}{CA}$=$\frac{CQ}{CB}$��$\frac{CP}{CB}$=$\frac{CQ}{CA}$��
����$\frac{2t}{8}$=$\frac{6-t}{6}$����$\frac{2t}{6}$=$\frac{6-t}{8}$��
���t=$\frac{12}{5}$����t=$\frac{18}{11}$��
��ˣ�����$\frac{12}{5}$���$\frac{18}{11}$�룬��OCQ���ACB���ƣ�
�� 3���п��ܣ�
�ɹ��ɶ�����AB=10��
��CDΪ��ACB�����ߣ�
���ACD=��A����BCD=��B��
��PQ��CD��
���CPQ=��B��
���PCQ�ס�BCA��
��$\frac{PC}{BC}$=$\frac{CQ}{AC}$��$\frac{2y}{6}$=$\frac{6-y}{8}$��
���y=$\frac{18}{11}$��
��ˣ�����$\frac{18}{11}$�룬PQ��CD��
���� ���⿼����һԪ���η��̵�Ӧ�ã����������ε��ж������ʣ������ε���������ɶ�����ֱ�������Ρ����������ε����ʣ�����ؼ���Ҫ������Ŀ����˼��������Ŀ�������������ҳ����ʵĵ�����ϵ���г����̣�����⣮


 �����Ƹ���ʦ����ϵ�д�
�����Ƹ���ʦ����ϵ�д� ��ͨ����ͬ����ϰ��ϵ�д�
��ͨ����ͬ����ϰ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
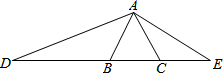 ��ͼ����ABC�ǵȱ������Σ�DΪCB�ӳ�����һ�㣬EΪBC�ӳ����ϵ㣬�ҡ�DAE=120��
��ͼ����ABC�ǵȱ������Σ�DΪCB�ӳ�����һ�㣬EΪBC�ӳ����ϵ㣬�ҡ�DAE=120���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
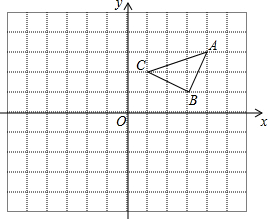 ��ͼ����������ABC������ƽ��5����λ���ȣ�������ƽ��4����λ���ȵõ�������A1B1C1��
��ͼ����������ABC������ƽ��5����λ���ȣ�������ƽ��4����λ���ȵõ�������A1B1C1���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 a��b������������ʾ�ĵ���ͼ��ʾ������$\sqrt{{a}^{2}b}$=-a$\sqrt{b}$��
a��b������������ʾ�ĵ���ͼ��ʾ������$\sqrt{{a}^{2}b}$=-a$\sqrt{b}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
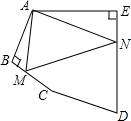 ��ͼ���������ABCDE�У���BAE=136�㣬��B=��E=90�㣬��BC��DE�Ϸֱ���һ��M��N��ʹ�á�AMN���ܳ���Сʱ�����AMN+��ANM�Ķ���Ϊ88�㣮
��ͼ���������ABCDE�У���BAE=136�㣬��B=��E=90�㣬��BC��DE�Ϸֱ���һ��M��N��ʹ�á�AMN���ܳ���Сʱ�����AMN+��ANM�Ķ���Ϊ88�㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | �ڡ�AOB�� | B�� | �ڡ�AOB�� | C�� | �ڡ�AOB���ڻ��� | D�� | �п�����OA�غ� |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com