
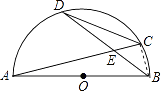
【题目】半圆O的直径AB=9,两弦AC、BD相交于点E,弦CD= ![]() ,且BD=7,则DE=
,且BD=7,则DE=
【答案】3 ![]()
【解析】根据圆周角定理得出的两组相等的对应角,易证得△AEB∽△DEC,根据CD、AB的长,即可求出两个三角形的相似比;设BE=x,则DE=7-x,然后根据相似比表示出AE、EC的长,连接BC,首先在Rt△BEC中,根据勾股定理求得BC的表达式,然后在Rt△ABC中,由勾股定理求得x的值,进而可求出DE的长.
∵∠D=∠A,∠DCA=∠ABD,
∴△AEB∽△DEC;
∴ ![]() ;
;
设BE=x,则DE=7-x,EC= ![]() x,AE=
x,AE= ![]() (7-x);
(7-x);
连接BC,则∠ACB=90°;
Rt△BCE中,BE=x,EC= ![]() x,则BC=
x,则BC= ![]() x;
x;
在Rt△ABC中,AC=AE+EC= ![]() -
- ![]() x,BC=
x,BC= ![]() x;
x;
由勾股定理,得:AB2=AC2+BC2,
即:92=( ![]() -
- ![]() x)2+(
x)2+( ![]() x)2,
x)2,
整理,得x2-14x+31=0,
解得:x1=7+3 ![]() (不合题意舍去),x2=7-3
(不合题意舍去),x2=7-3 ![]()
则DE=7-x=3![]() .
.
【考点精析】本题主要考查了相似三角形的判定与性质的相关知识点,需要掌握相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方才能正确解答此题.


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中
(1)写出点A,B,C的坐标.
(2)作出△ABC关于y轴的对称图形△A1B1C1.
(3)写出点A1,B1,C1的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c的开口向下,与x轴和y轴分别交于点A(﹣4,0)和点B(0,2),过点B作BC⊥AB交抛物线于点C,连接AC,且∠BAC=∠BAO. 
(1)求BC的长;
(2)求抛物线的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,过原点O的直线与双曲线y= ![]() 交于A、B两点,过点B作BC⊥x轴,垂足为C,连接AC,若S△ABC=5,则k的值是( )
交于A、B两点,过点B作BC⊥x轴,垂足为C,连接AC,若S△ABC=5,则k的值是( ) 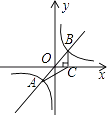
A.![]()
B.![]()
C.5
D.10
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,在平面直角坐标系中,点![]() 的坐标分别是
的坐标分别是![]() 且
且![]() .
.

(1)求![]() 的值;
的值;
(2)在![]() 轴上是否存在点
轴上是否存在点![]() ,使三角形
,使三角形![]() 的面积是
的面积是![]() ?若存在,求出点
?若存在,求出点![]() 的坐标;若不存在,请说明理由;
的坐标;若不存在,请说明理由;
(3)已知点![]() 是
是![]() 轴正半轴上一点,且到
轴正半轴上一点,且到![]() 轴的距离为
轴的距离为![]() ,若
,若![]() 点沿
点沿![]() 轴负半轴方向以每秒
轴负半轴方向以每秒![]() 个单位长度平移至点
个单位长度平移至点![]() ,当运动时间
,当运动时间![]() 为多少秒时,四边形
为多少秒时,四边形![]() 的面积
的面积![]() 为
为![]() 个平方单位?并写出此时点
个平方单位?并写出此时点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阿成全班32人参加学校的英文听力测验,如图是全校与全班成绩的盒状图.若阿成的成绩恰为全校的第65百分位数,则下列关于阿成在班上排名的叙述,何者正确?( )

A. 在第2~7名之间 B. 在第8~15名之间
C. 在第16~21名之间 D. 在第21~25名之间
查看答案和解析>>
科目:初中数学 来源: 题型:
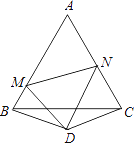
【题目】如图,△ABC是边长为1的等边三角形,△BDC是顶角∠BDC=120°的等腰三角形,以D为顶点作一个60°角,角的两边分别交AB,AC于M,N,连接MN.求△AMN的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
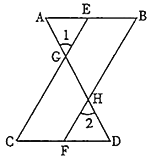
【题目】完成下面的证明:
如图,已知![]() ,
,![]() ,可推得
,可推得![]() .
.
理由如下:∵![]() (已知),
(已知),
且![]() ( )
( )
∴![]() (等量代换)
(等量代换)
∴________∥________( )
∴∠________![]() ( )
( )
又∵![]() (已知)
(已知)
∴![]() ( )
( )
∴![]() ( )
( )
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com