
【题目】如图,S为一个点光源,照射在底面半径和高都为2m的圆锥体上,在地面上形成的影子为EB,且∠SBA=30°。(以下计算结果都保留根号)
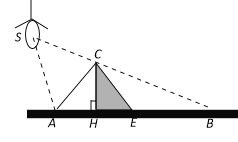
(1)、求影子EB的长;
(2)、若∠SAC=60°,求光源S离开地面的高度。
【答案】(1)、![]() ;(2)、2+
;(2)、2+![]()
【解析】
试题分析:(1)、根据题意得出CH=HE=2m;根据∠SBA=30°得出HB=![]() ,从而根据BE=BH-HE得出答案;(2)、作CD⊥SA于点D,根据Rt△ACD的三角函数得出CD的长度,然后得出∠DSC的度数,从而求出SC的长度,最后求出SB的长度,根据SF=
,从而根据BE=BH-HE得出答案;(2)、作CD⊥SA于点D,根据Rt△ACD的三角函数得出CD的长度,然后得出∠DSC的度数,从而求出SC的长度,最后求出SB的长度,根据SF=![]() SB得出答案.
SB得出答案.
试题解析:(1)、∵圆锥的底面半径和高都为2m,
∴CH=HE=2m,
∵∠SBA=30°,
∴HB=![]() m,
m,
∴影长BE=BH﹣HE=![]() (m);
(m);
(2)、作CD⊥SA于点D,
在Rt△ACD中,得CD=ACcos30°=![]() AC=
AC=![]() ,
,
∵∠SBA=30°,∠SAB=∠SAC+∠BAC=60°+45°=105°,
∴∠DSC=45°,∴SC= ,
,
∴SB=2![]() +BC=2
+BC=2![]() +4,
+4,
∴SF=![]() SB=(
SB=(![]() +2)m,
+2)m,
答:光源S离开地面的高度为(2+![]() )m。
)m。


科目:初中数学 来源: 题型:
【题目】下列各组数中,不相等的一组是( )
A. -(+7), -|-7| B. -(+7),-|+7| C. +(-7), -(+7) D. +(+7), -|-7|
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,把点P(﹣3,2)绕原点O顺时针旋转180°,所得到的对应点P′的坐标为( )
A.(3,2)
B.(2,﹣3)
C.(﹣3,﹣2)
D.(3,﹣2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 与x轴交于点B,与
与x轴交于点B,与![]() 轴交于点
轴交于点![]() ,已知二次函数的图象经过点B、
,已知二次函数的图象经过点B、![]() 和点
和点![]() 。
。
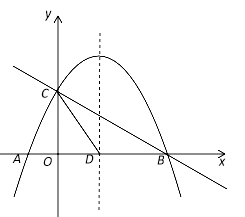
(1)求该二次函数的关系式;
(2)点E是线段BC上的一个动点,过点E作x轴的垂线与抛物线相交于点F,当点E运动到什么位置时,四边形CDBF的面积最大?求出四边形CDBF的最大面积及此时E点的坐标。
(3)若抛物线的对称轴与x轴的交点为点D,则在抛物线的对称轴上是否存在点P,使△PCD是以CD为腰的等腰三角形?如果存在,直接写出P点的坐标;如果不存在,请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,∠BAC=40°,将△ABC绕点A按逆时针方向旋转100°.得到△ADE,连接BD,CE交于点F.
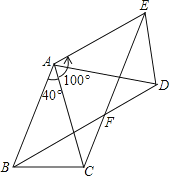
(1)求证:△ABD≌△ACE;
(2)求∠ACE的度数;
(3)求证:四边形ABFE是菱形
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com