（本小题满分10分）如图：已知⊙O的直径CD为2，
的度数为60°，点B是的中点，在直径CD上作出点P，使BP+AP的值最小，则BP+AP的最小值为多少？
．
【解析】
试题分析：作B关于CD的对称点E，则E正好在圆周上连接OA、OB、OE、AE，AE交CD于P，则AP+BP最短，根据
的度数为60°，点B是的中点计算出，∠AOB=∠COB=30°，然后再证明△OAE是等腰直角三角形，再利用勾股定理可得答案．
试题解析：作B关于CD的对称点E，则E正好在圆周上，
连接OA、OB、OE、AE，AE交CD于P，则AP+BP最短，
∵的度数为60°，点B是的中点，∴
，且
的度数是30°，∴∠AOB=∠COB=30°，
∵B关于CD的对称点是E，∴弧BE的度数是60°，∴∠AOE=90°，
∵OA=OE=
CD=1，∴△OAE是等腰直角三角形，
由勾股定理得：AE=．
考点：1．轴对称-最短路线问题；2．勾股定理；3．垂径定理．
作业辅导系列答案科目：初中数学 来源： 题型：
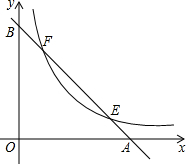如图，已知直线y=-x+2分别与x轴，y轴交于A，B两点，与双曲线y=| k |
| x |
| A、-1 | ||
| B、1 | ||
C、
| ||
D、
|
查看答案和解析>>
科目：初中数学 来源：2014-2015学年浙江省杭州市联盟学校九年级上学期期中考试数学试卷（解析版） 题型：解答题
（本小题满分10分）在关于x，y的二元一次方程组
中．
（1）若
，求方程组的解；
（2）若
，当
为何值时，S有最小值．
查看答案和解析>>
科目：初中数学 来源：2014-2015学年浙江省杭州市萧山地区九年级上学期期中考试数学试卷（解析版） 题型：解答题
(本小题满分8分）已知函数y=mx2-6x+1（m是常数）．
（1）求证：不论m为何值，该函数的图象都经过y轴上的一个定点；
（2）若该函数的图象与x轴只有一个交点，求m的值．
查看答案和解析>>
科目：初中数学 来源：2014-2015学年浙江省九年级上学期第二次月考数学试卷（解析版） 题型：解答题
（本题10分）如图，在平面直角坐标系xOy中，边长为
的正方形ABCD的顶点A，D分别在x轴、y轴的正半轴上，点A的坐标（1, 0）.
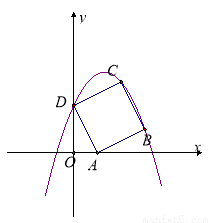
（1）写出点B的坐标( , )；点C的坐标( , )；
（2）若抛物线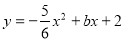
恰好经过B，C，D三点．
①求b的值；
②根据函数的图象，求出当y＞0时x的取值范围．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
，当x≥3时，y随x的增大而减小，则a= ．（写出一个即可）
；
的度数是 