
【题目】如图,正方形![]() 的边长为
的边长为![]() ,
, ![]() 、
、![]() 、
、![]() 分别是
分别是![]() 、
、![]() 、
、![]() 上的动点,且
上的动点,且![]() .
.
(![]() )求证:四边形
)求证:四边形![]() 是正方形.
是正方形.
(![]() )判断直线
)判断直线![]() 是否经过某一定点,说明理由.
是否经过某一定点,说明理由.

【答案】(1)证明见解析;(2)![]() 必过
必过![]() 中点这个点,理由见解析.
中点这个点,理由见解析.
【解析】试题分析:(1)由正方形的性质得出∠A=∠B=∠C=∠D=90°,AB=BC=CD=DA,证出AH=BE=CF=DG,由SAS证明△AEH≌△BFE≌△CGF≌△DHG,得出EH=FE=GF=GH,∠AEH=∠BFE,证出四边形EFGH是菱形,再证出∠HEF=90°,即可得出结论;(2)直线EG经过正方形ABCD的中心, 连接BD交EG于点O,易证△EOB≌△GOD.可得BO=DO即点O为BD的中点.所以直线EG经过正方形ABCD的中心.
试题解析:
(![]() )∵四边形
)∵四边形![]() 是正方形.
是正方形.
∴![]() ,
, ![]() .
.
∵![]() .
.
∴![]() .
.
∴![]() ≌
≌![]() ≌
≌![]() ≌
≌![]() .
.
∴![]() ,
, ![]() .
.
∴四边形![]() 是菱形.
是菱形.
∵![]() ,
, ![]() .
.
∴![]() .
.
∴![]() .
.
∵四边形![]() 是菱形,
是菱形, ![]() .
.
∴四边形![]() 是正方形.
是正方形.
(![]() )直线
)直线![]() 经过正方形
经过正方形![]() 的中心,理由如下:
的中心,理由如下:
连接![]() 交
交![]() 于点
于点![]() .
.
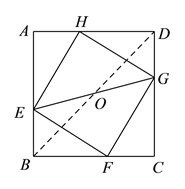
∵四边形![]() 是正方形.
是正方形.
∴![]() .
.
∴![]() .
.
∵![]() ,
, ![]() ,
, ![]() .
.
∴![]() ≌
≌![]() .
.
∴![]() ,即点
,即点![]() 为
为![]() 的中点.
的中点.
∴直线![]() 经过正方形
经过正方形![]() 的中心.
的中心.


 应用题作业本系列答案
应用题作业本系列答案科目:初中数学 来源: 题型:
【题目】我们知道“在同一平面内,经过直线外一点有且只有一条直线与已知直线平行”,

小伟同学想通过“同位角相等,两直线平行”作出图形,具体作法是,过点P任意作一条直线a与直线l相交,再以P为顶点作一个角,直线a为角的一边所在直线,则角的另一边所在直线与直线l平行.
(1)请你参照小伟同学的作法,帮他完成剩余的作图(保留作图痕迹,不写作法)
(2)你还有其它办法吗?请在备用图中完成(只需一种即可,保留作图痕迹,不写作法)


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中,错误的是( )
A. 线段是轴对称图形
B. 等边三角形有3条对称轴
C. 角只有一条对称轴,是这个角的角平分线
D. 底与腰不相等的等腰三角形只有一条对称轴
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知射线OC上的任意一点到∠AOB的两边的距离都相等,点D、E、F分别为边OC、OA、OB上,如果要想证得OE=OF,只需要添加以下四个条件中的某一个即可,请写出所有可能的条件的序号__________.
①∠ODE=∠ODF;②∠OED=∠OFD;③ED=FD;④EF⊥OC.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com