【题目】当我们利用2种不同的方法计算同一图形的面积时，可以得到一个等式．例如，由图1，可得等式：（a+2b）（a+b）=a2+3ab+2b2 ．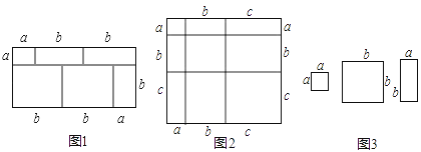
（1）由图2，可得等式：
（2）利用（1）中所得到的结论，解决下面的问题：已知 a+b+c=11，ab+bc+ac=38，求a2+b2+c2的值；
（3）利用图3中的纸片（足够多），画出一种拼图，使该拼图可用来验证等式：2a2+5ab+2b2=（2a+b）（a+2b）；
（4）小明用2 张边长为a 的正方形，3 张边长为b的正方形，5 张边长分别为a、b 的长方形纸片重新拼出一个长方形，那么该长方形较长的一条边长为

参考答案：

【答案】
（1）
（2）解：
（3）解：如图所示
（4）2a+3b
【解析】（1） ；(4) 根据题意得：2a2+5ab+3b2=（2a+3b）(a+b)，则较长的一边为2a+3b。
【考点精析】解答此题的关键在于理解多项式乘多项式的相关知识，掌握多项式与多项式相乘，先用一个多项式的每一项乘另外一个多项式的每一项，再把所得的积相加．

关闭