练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】把抛物线y＝﹣2（x﹣2）2+3先向右平移1个单位长度，再向上平移2个单位长度后，所得函数的表达式为（　　）

    A.y＝﹣2（x﹣1）2+2B.y＝﹣2（x+1）2+2

    C.y＝﹣2（x﹣3）2+5D.y＝2（x﹣3）2+5

    【答案】C

    【解析】

    由函数图象平移性质：上加下减问题可解.

    解：把抛物线y＝﹣2（x﹣2）2+3先向右平移1个单位长度，再向上平移2个单位长度后，所得函数的表达式为y＝﹣2（x﹣3）2+5，

    故选：C．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】光明中学七（1）班40个同学每10人一组，每人做10次抛掷两枚硬币的实验，想想看“出现两个正面”的频率是否会逐渐稳定下来，得到了下面40个实验结果。

    第一组学生学号

    101

    102

    103

    104

    105

    106

    107

    108

    109

    110

    两个正面成功次数

    1

    2

    3

    3

    3

    3

    3

    6

    3

    3

    第二组学生学号

    111

    112

    113

    114

    115

    116

    117

    118

    119

    120

    两个正面成功次数

    1

    1

    3

    2

    3

    4

    2

    3

    3

    3

    第三组学生学号

    121

    122

    123

    124

    125

    126

    127

    128

    129

    130

    两个正面成功次数

    1

    0

    3

    1

    3

    3

    3

    2

    2

    2

    第四组学生学号

    131

    132

    133

    134

    135

    136

    137

    138

    139

    140

    两个正面成功次数

    2

    2

    1

    4

    2

    4

    3

    2

    3

    3


    （1）学号为113的同学在他10次实验中，成功了几次？成功率是多少？他是他所在小组同学中成功率最高的人吗？
    （2）学号为116和136的两位同学在10次实验中成功率一样吗？如果他们两人再做10次实验，成功率依然会一样吗？
    （3）怎么计算每一组学生的集体成功率？哪一组成功率最高？
    （4）累计每个学生的实验结果，完成下面的“出现两个正面”的频数、频率随抛掷次数变化统计表，如果把这张表画成相应的图，你会看到什么？

    抛掷次数

    50

    100

    150

    200

    250

    300

    350

    400

    出现两个正面的频数

    出现两个正面的频率

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在对某社会机构的调查中收集到以下数据，你认为最能够反映该机构年龄特征的统计量是（　　）

    年龄

    13

    14

    15

    25

    28

    30

    35

    其他

    人数

    30

    533

    17

    12

    20

    9

    2

    3

    A. 平均数 B. 众数 C. 方差 D. 标准差

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】当我们利用2种不同的方法计算同一图形的面积时，可以得到一个等式．例如，由图1，可得等式：（a+2b）（a+b）=a2+3ab+2b2 ．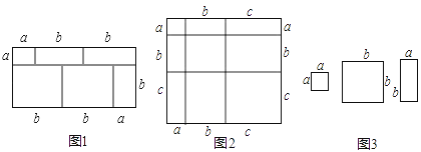
    （1）由图2，可得等式：
    （2）利用（1）中所得到的结论，解决下面的问题：已知 a+b+c=11，ab+bc+ac=38，求a2+b2+c2的值；
    （3）利用图3中的纸片（足够多），画出一种拼图，使该拼图可用来验证等式：2a2+5ab+2b2=（2a+b）（a+2b）；
    （4）小明用2 张边长为a 的正方形，3 张边长为b的正方形，5 张边长分别为a、b 的长方形纸片重新拼出一个长方形，那么该长方形较长的一条边长为

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】小河两岸边各有一棵树，分别高30尺和20尺，两树的距离是50尺，每棵树的树顶上都停着一只鸟．忽然，两只鸟同时看见水面上游出一条鱼，它们立刻飞去抓鱼，速度相同，并且同时到达目标．则这条鱼出现的地方离开比较高的树的距离为尺．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】用正方形硬纸板做三棱柱盒子，每个盒子由3个矩形侧面和2个正三角形底面组成，硬纸板以如图两种方法裁剪（裁剪后边角料不再利用）．
    A方法：剪6个侧面； B方法：剪4个侧面和5个底面．

    现有19张硬纸板，裁剪时x张用A方法，其余用B方法．
    （1）用x的代数式分别表示裁剪出的侧面和底面的个数；
    （2）若裁剪出的侧面和底面恰好全部用完，问能做多少个盒子？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知x2-2x-8=0，则6x-3x2+18的值是（ ）

    A. -6 B. 6 C. 42 D. -42

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，在等腰直角△ABC中，AB=AC，∠BAC=90°，小敏将一块三角板中含45°角的顶点放在A上，从AB边开始绕点A逆时针旋转一个角α，其中三角板斜边所在的直线交直线BC于点D，直角边所在的直线交直线BC于点E．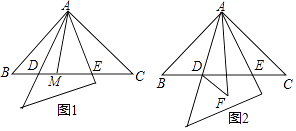

    （1）小敏在线段BC上取一点M，连接AM，旋转中发现：若AD平分∠BAM，则AE也平分∠MAC．请你证明小敏发现的结论；
    （2）当0°＜α≤45°时，小敏在旋转中还发现线段BD、CE、DE之间存在如下等量关系：BD2+CE2=DE2 ． 同组的小颖和小亮随后想出了相同的方法进行解决：将△ABD沿AD所在的直线对折得到△ADF（如图2）；请证明小敏的发现的是正确的．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，点A，O，B在同一条直线上，∠AOC=∠BOC，若∠1=∠2，则图中与∠2互余的角共有（ ）对

    A.2
    B.3
    C.4
    D.5

    查看答案和解析>>

    同步练习册答案