
【题目】平面直角坐标系![]() 中,横坐标为a的点 A在反比例函数
中,横坐标为a的点 A在反比例函数![]() 的图象上,点
的图象上,点![]() 与点
与点![]() 关于点
关于点![]() 对称,一次函数
对称,一次函数![]() 的图象经过点
的图象经过点![]()
(1)设![]() ,点
,点![]() (4,2)在函数
(4,2)在函数![]() ,
,![]() 的图像上.
的图像上.
①分别求函数![]() ,
,![]() 的表达式;
的表达式;
②直接写出使![]() 成立的
成立的![]() 的范围;
的范围;
(2)如图①,设函数![]() ,
,![]() 的图像相交于点
的图像相交于点![]() ,点
,点![]() 的横坐标为
的横坐标为![]() ,△
,△![]() 的面积为16,求
的面积为16,求![]() 的值;
的值;
(3)设![]() ,如图②,过点
,如图②,过点![]() 作
作![]() 轴,与函数
轴,与函数![]() 的图像相交于点
的图像相交于点![]() ,以
,以![]() 为一边向右侧作正方形
为一边向右侧作正方形![]() ,试说明函数
,试说明函数![]() 的图像与线段
的图像与线段![]() 的交点
的交点![]() 一定在函数
一定在函数![]() 的图像上.
的图像上.

【答案】(1)①![]() ;②2<x<4;(2)k=6;(3)见解析.
;②2<x<4;(2)k=6;(3)见解析.
【解析】
(1)由已知代入点坐标即可;
(2)面积问题可以转化为△AOB面积,用a、k表示面积问题可解;
(3)设出点A、A′坐标,依次表示AD、AF及点P坐标.
(1)解:∵点B(4,2) 在函数![]() ,
,![]() 的图像上.∴k=4×2=8∴
的图像上.∴k=4×2=8∴![]()
∵点A在![]() 上∴x=a=2,y=4∴点A(2,4)
上∴x=a=2,y=4∴点A(2,4)
∵A和点A'关于原点对称
∴点A'的坐标为(-2,-4)
∵一次函数y2=mx+n的图像经过点A'和点B![]()
解得:![]() ∴y2=x-2;
∴y2=x-2;
②由图像可知,当![]() 时,y1=
时,y1=![]() 图象在y2=x-2图象上方,且两函数图象在x轴上方,
图象在y2=x-2图象上方,且两函数图象在x轴上方,
∴由图象得: 2<x<4;
(2)解:)分别过点A、B作AC⊥x轴于点C,BD⊥x轴于点D,连BO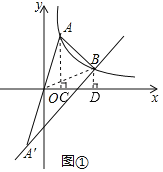
∵O为AA′中点
S△AOB=![]() S△ABA′=8
S△ABA′=8
∵点A、B在双曲线上
∴S△AOC=S△BOD
∴S△AOB=S四边形ACDB=8
由已知点A、B坐标都表示为(a,![]() )(3a,
)(3a,![]() )
)
∴![]() ×(
×(![]() +
+![]() )×2a=8
)×2a=8
解得k=6;
(3)解:设A(a ,![]() ),则A′(﹣a ,﹣
),则A′(﹣a ,﹣![]() ),代入
),代入![]() 得
得 ![]() ,
,
∴![]() ,
,
∴D(a,![]() )
)
∴AD=![]() ,
,
∵AD=AF,
∴![]() ,代入
,代入![]() 得
得![]() ,即P(
,即P(![]() ,
,![]() )
)
将点P横坐标代入![]() 得纵坐标为
得纵坐标为![]() ,可见点P一定在函数
,可见点P一定在函数![]() 的图像上.
的图像上.
故答案为(1)①![]() ;②2<x<4;(2)k=6;(3)见解析.
;②2<x<4;(2)k=6;(3)见解析.


科目:初中数学 来源: 题型:
【题目】网瘾低龄化问题已经引起社会各界的高度关注,有关部门在全国范围内对12﹣35岁的网瘾人群进行了简单的随机抽样调查,绘制出以下两幅统计图.

请根据图中的信息,回答下列问题:
(1)这次抽样调查中共调查了 人;
(2)请补全条形统计图;
(3)扇形统计图中18﹣23岁部分的圆心角的度数是 ;
(4)据报道,目前我国12﹣35岁网瘾人数约为2000万,请估计其中12﹣23岁的人数
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义运算a![]() b=a(1-b),下面给出了关于这种运算的四个结论:
b=a(1-b),下面给出了关于这种运算的四个结论:
①2![]() (-2)=6 ②a
(-2)=6 ②a![]() b=b
b=b![]() a
a
③若a+b=0,则(a![]() a)+(b
a)+(b![]() b)=2ab ④若a
b)=2ab ④若a![]() b=0,则a=0.
b=0,则a=0.
其中正确结论的序号是 (填上你认为所有正确结论的序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】模具厂计划生产面积为4,周长为m的矩形模具.对于m的取值范围,小亮已经能用“代数”的方法解决,现在他又尝试从“图形”的角度进行探究,过程如下:
(1)建立函数模型
设矩形相邻两边的长分别为x,y,由矩形的面积为4,得![]() ,即
,即![]() ;由周长为m,得
;由周长为m,得![]() ,即
,即![]() .满足要求的
.满足要求的![]() 应是两个函数图象在第 象限内交点的坐标.
应是两个函数图象在第 象限内交点的坐标.
(2)画出函数图象
函数![]() 的图象如图所示,而函数
的图象如图所示,而函数![]() 的图象可由直线
的图象可由直线![]() 平移得到.请在同一直角坐标系中直接画出直线
平移得到.请在同一直角坐标系中直接画出直线![]() .
.
(3)平移直线![]() ,观察函数图象
,观察函数图象
①当直线平移到与函数![]() 的图象有唯一交点
的图象有唯一交点![]() 时,周长m的值为 ;
时,周长m的值为 ;
②在直线平移过程中,交点个数还有哪些情况?请写出交点个数及对应的周长m的取值范围.
(4)得出结论
若能生产出面积为4的矩形模具,则周长m的取值范围为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
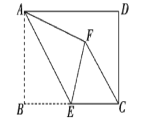
【题目】如图,在矩形ABCD中,AB=4,BC=6,点E为BC的中点,将△ABE沿AE折叠,使点B落在矩形内点F处,连接CF,则CF的长度为_____
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校组织![]() 名同学和
名同学和![]() 名教师参加校外学习交流活动现打算选租大、小两种客车,大客车载客量为
名教师参加校外学习交流活动现打算选租大、小两种客车,大客车载客量为![]() 人/辆,小客车载客量为
人/辆,小客车载客量为![]() 人/辆
人/辆
(1)学校准备租用![]() 辆客车,有几种租车方案?
辆客车,有几种租车方案?
(2)在(1)的条件下,若大客车租金为![]() 元/辆,小客车租金为
元/辆,小客车租金为![]() 元/辆,哪种租车方案最省钱?
元/辆,哪种租车方案最省钱?
(3)学校临时增加![]() 名学生和
名学生和![]() 名教师参加活动,每辆大客车有2名教师带队,每辆小客车至少有
名教师参加活动,每辆大客车有2名教师带队,每辆小客车至少有![]() 名教师带队.同学先坐满大客车,再依次坐满小客车,最后一辆小客车至少要有
名教师带队.同学先坐满大客车,再依次坐满小客车,最后一辆小客车至少要有![]() 人,请你帮助设计租车方案
人,请你帮助设计租车方案
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,DE⊥AB于E,DF⊥AC于F,若BD=CD,BE=CF.
(1)求证:AD平分∠BAC.
(2)写出AB+AC与AE之间的等量关系,并说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com