
【题目】如下图,点![]() 是
是![]() 的中点,
的中点,![]() ,
,![]() ,
,![]() 平分
平分![]() ,下列结论:
,下列结论:
①![]() ②
②![]() ③
③![]() ④
④![]()
四个结论中成立的是( )
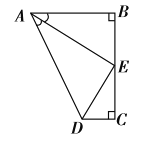
A.①②④B.①②③C.②③④D.①③④
【答案】A
【解析】
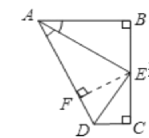
过E作EF⊥AD于F,易证得Rt△AEF≌Rt△AEB,得到BE=EF,AB=AF,∠AEF=∠AEB;而点E是BC的中点,得到EC=EF=BE,则可证得Rt△EFD≌Rt△ECD,得到DC=DF,∠FDE=∠CDE,也可得到AD=AF+FD=AB+DC,∠AED=∠AEF+∠FED=![]() ∠BEC=90°,即可判断出正确的结论.
∠BEC=90°,即可判断出正确的结论.
过E作EF⊥AD于F,如图,
∵AB⊥BC,AE平分∠BAD,
∴Rt△AEF≌Rt△AEB
∴BE=EF,AB=AF,∠AEF=∠AEB;
而点E是BC的中点,
∴EC=EF=BE,所以③错误;
∴Rt△EFD≌Rt△ECD,
∴DC=DF,∠ADE=∠CDE,所以②正确;
∴AD=AF+FD=AB+DC,所以④正确;
∴∠AED=∠AEF+∠FED=![]() ∠BEC=90°,所以①正确.
∠BEC=90°,所以①正确.
故选A.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD为长方形,C点在x轴,A点在y轴上,D点坐标是(0,0),B点坐标是(3,4),长方形ABCD沿直线EF折叠,点A落在BC边上的G处,E、F分别在AD、AB上,F(2,4).
(1)求G点坐标;
(2)△EFG的面积为 (直接填空);
(3)点N在x轴上,直线EF上是否存在点M,使以M、N、F、G为顶点的四边形是平行四边形?若存在,请直接写出M点的纵坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,现有一个可以自由转动的转盘,盘面被平均分成6等份,分别标有2,3,4,5,6,7这六个数字.转动转盘,当转盘停止时,指针指向区域所标示的数字即为转出的数字(若指针落在相邻两扇形交界处,重新转动转盘).

(1)转出数字10是________(填“随机事件”“必然事件”“不可能事件”中的一个);
(2)转出的数字大于3的概率是_________;
(3)现有两张分别写有3和4的卡片,随机转动转盘,转盘停止后记下转出的数字,该数字与两张卡片上的数字分别作为三条线段的长度.
①这三条线段以有构成三角形的概率是___________;
②这三条线段能构成等腰三角形的概率是_____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在![]() 和
和![]() 中
中![]() ,
,![]() ,
,![]() ,连接
,连接![]() ,
,![]() ,
,![]() 绕点
绕点![]() 自由旋转.
自由旋转.

(1)当![]() 在
在![]() 边上时,
边上时,
①线段![]() 和线段
和线段![]() 的关系是____________________;
的关系是____________________;
②若![]() ,则
,则![]() 的度数为____________;
的度数为____________;
(2)如图2,点![]() 不在
不在![]() 边上,
边上,![]() ,
,![]() 相交于点
相交于点![]() ,(l)问中的线段
,(l)问中的线段![]() 和线段
和线段![]() 的关系是否仍然成立?并说明理由.
的关系是否仍然成立?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】圆柱的底面半径是2cm,当圆柱的高h(cm)由大到小变化时,圆柱的体积V(cm3)随之发生变化。
(1)在这个变化过程中,自变量和因变量各是什么?
(2)在这个变化过程中,写出圆柱的体积为V与高h之间的关系式?
(3)当h由5cm变化到10cm时,V是怎样变化的?
查看答案和解析>>
科目:初中数学 来源: 题型:
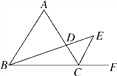
【题目】如图,△ABC是等边三角形,CE是∠ACB的外角平分线,点D在AC上,连接BD并延长交CE于点E.
(1)求证:△ABD∽△CED;
(2)若AB=6,AD=2CD,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平面直角坐标系![]() 中,横坐标为a的点 A在反比例函数
中,横坐标为a的点 A在反比例函数![]() 的图象上,点
的图象上,点![]() 与点
与点![]() 关于点
关于点![]() 对称,一次函数
对称,一次函数![]() 的图象经过点
的图象经过点![]()
(1)设![]() ,点
,点![]() (4,2)在函数
(4,2)在函数![]() ,
,![]() 的图像上.
的图像上.
①分别求函数![]() ,
,![]() 的表达式;
的表达式;
②直接写出使![]() 成立的
成立的![]() 的范围;
的范围;
(2)如图①,设函数![]() ,
,![]() 的图像相交于点
的图像相交于点![]() ,点
,点![]() 的横坐标为
的横坐标为![]() ,△
,△![]() 的面积为16,求
的面积为16,求![]() 的值;
的值;
(3)设![]() ,如图②,过点
,如图②,过点![]() 作
作![]() 轴,与函数
轴,与函数![]() 的图像相交于点
的图像相交于点![]() ,以
,以![]() 为一边向右侧作正方形
为一边向右侧作正方形![]() ,试说明函数
,试说明函数![]() 的图像与线段
的图像与线段![]() 的交点
的交点![]() 一定在函数
一定在函数![]() 的图像上.
的图像上.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com