
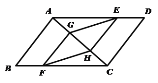
【题目】已知:在平行四边形ABCD中,点E、F分别在AD和BC上,点G、H在AC上,且AE=CF,AH=CG.
求证:四边形EGFH是平行四边形.
 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案科目:初中数学 来源: 题型:
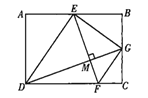
【题目】如图,点E是矩形ABCD的边AB的中点,点F是边CD上一点,连接ED,EF,ED平分∠AEF,过点D作DG⊥EF于点M,交BC于点G,连接GE,GF,若FG∥DE,则![]() 的值是( )
的值是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校锅炉旁建有一个储煤库,开学初购进一批煤,现在知道:按每天用煤0.6吨计算,一学期(按150天计算)刚好用完.若每天的耗煤量为 x吨,那么这批煤能维持 y天.
(1)则 y与 x之间有怎样的函数关系?
(2)画出此函数的图象.
(3)若每天节约0.1吨,则这批煤能多维持多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,每个图案都由若干个“●”组成,其中第①个图案中有7个“●”,第②个图案中有13个“●”,…,则第⑨个图案中“●”的个数为( )

A.87B.91C.103D.111
查看答案和解析>>
科目:初中数学 来源: 题型:
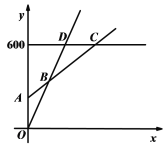
【题目】某水上乐园普通票价20元/张,假期为了促销,新推出两种优惠卡:贵宾卡售价600元/张,每次凭卡不再收费;会员卡售价200元/张,每次凭卡另收10元.暑期普通票正常出售,两种优惠卡仅限暑期使用,不限次数.设游泳x次时,所需总费用为y元.
(1)分别写出假期选择会员卡、普通票消费时,y与x之间的函数关系式;
(2)在同一个坐标系中,若三种消费方式对应的函数图象如图所示,请求出点A、B、C、D的坐标,并直接写出选择哪种消费方式更合算.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠ABC=90°,D是BC的中点,E是AD的中点,过点A作AF∥BC交BE的延长线于点F.
(1)证明四边形ADCF是菱形;
(2)若AC=4,AB=5,求菱形ADCF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】网瘾低龄化问题已经引起社会各界的高度关注,有关部门在全国范围内对12﹣35岁的网瘾人群进行了简单的随机抽样调查,绘制出以下两幅统计图.

请根据图中的信息,回答下列问题:
(1)这次抽样调查中共调查了 人;
(2)请补全条形统计图;
(3)扇形统计图中18﹣23岁部分的圆心角的度数是 ;
(4)据报道,目前我国12﹣35岁网瘾人数约为2000万,请估计其中12﹣23岁的人数
查看答案和解析>>
科目:初中数学 来源: 题型:
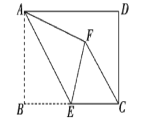
【题目】如图,在矩形ABCD中,AB=4,BC=6,点E为BC的中点,将△ABE沿AE折叠,使点B落在矩形内点F处,连接CF,则CF的长度为_____
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com