Question

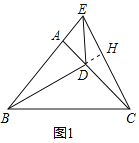
【题目】如图1，在和中，，，连接，，绕点自由旋转.

（1）当在边上时，

①线段和线段的关系是____________________；

②若，则的度数为____________；

（2）如图2，点不在边上，，相交于点，（l）问中的线段和线段的关系是否仍然成立？并说明理由.

Answer 1

【答案】（1）①BD=CE，BD⊥CE，②67.5°；（2）（1）问中的线段BD和线段CE的关系仍然成立

【解析】

（1）①延长BD交CE于H，证明△ABD≌△ACE，根据全等三角形的性质得到BD=CE，∠ABD=∠ACE，求出∠CHD=90°，得到BD⊥CE，得到答案；
②根据等腰三角形的性质得到∠ABC=∠ACB=45°，根据等腰三角形的性质、三角形的外角性质计算即可；
（2）仿照（1）①的作法证明即可．

解：（1）①延长BD交CE于H，

在△ABD和△ACE中，

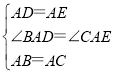
∴△ABD≌△ACE（SAS）
∴BD=CE，∠ABD=∠ACE，
∵∠ABD+∠ADB=90°，∠ADB=∠CDH，
∴∠DCH+∠CDH=90°，即∠CHD=90°，
∴BD⊥CE，
故答案为：BD=CE，BD⊥CE；

②BC=AD+AB=AE+AB=BE，
∴∠BEC=∠BCE，
∵∠BAC=90°，AB=AC，
∴∠ABC=∠ACB=45°，
∴∠BEC=∠BCE=67.5°，
∵BE=BC，BH⊥CE，
∴∠CBH=∠EBH=∠ACE，
∴∠ADB=∠DBC+∠DCB=∠ACE+∠DCB=67.5°，
故答案为：67.5°；

（2）（1）问中的线段BD和线段CE的关系仍然成立，
∵∠BAC=∠DAE=90°，
∴∠BAC+∠DAC=∠DAE+∠DAC，即∠BAD=∠CAE
理由如下：在△ABD和△ACE中，

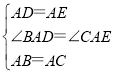
∴△ABD≌△ACE（SAS）
∴BD=CE，∠ABD=∠ACE，
∵∠ABD+∠ANB=90°，∠ANB=∠FNC，
∴∠ACF+∠DNC=90°，即∠CFN=90°，
∴BD⊥CE，
综上所述，BD=CE，BD⊥CE．