
【题目】如图,四边形ABCD为长方形,C点在x轴,A点在y轴上,D点坐标是(0,0),B点坐标是(3,4),长方形ABCD沿直线EF折叠,点A落在BC边上的G处,E、F分别在AD、AB上,F(2,4).
(1)求G点坐标;
(2)△EFG的面积为 (直接填空);
(3)点N在x轴上,直线EF上是否存在点M,使以M、N、F、G为顶点的四边形是平行四边形?若存在,请直接写出M点的纵坐标;若不存在,请说明理由.

【答案】(1)G点的坐标为![]() ;(2)
;(2)![]() ;(3)
;(3)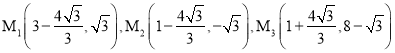
【解析】
(1)根据折叠性质可知FG=AF=2,而FB=AB-AF=1,则在Rt△BFG中,利用勾股定理求出BG的长,从而得到CG的长,从而得到G点坐标;
(2)由三角函数求出∠BFG=60°,得出∠AFE=∠EFG=60°,由三角函数求出AE=AFtan∠AFE=2,代入三角形面积公式计算即可;
(3)因为M、N均为动点,只有FG已经确定,所以可从此入手,按照FG为一边、FG为对角线的思路,顺序探究可能的平行四边形的形状.确定平行四边形的位置与形状之后,利用全等三角形求得M点的纵坐标,再利用直线解析式求出M点的横坐标,从而求得M点的坐标.
解:(1)∵B点坐标是(3,4),F(2,4),
∴AB=3,OA=BC=4,AF=2,
∴BF=AB-AF=1,
由折叠的性质得:△EFA≌△EFG,GF=AF=2,
∵四边形ABCD为矩形,
∴∠B=90°,
∴![]()
∴![]()
∴G点的坐标为![]()
(2)在Rt△BFG中,cos∠BFG=![]()
∴∠BFG=60°,
∴∠AFE=∠EFG=60°,
∴AE=AFtan∠AFE=2tan60°=![]()
∵△EFA的面积=![]()
∴△EFG的面积=![]()
故答案为:![]()
(3)若以M、N、F、G为顶点的四边形是平行四边形,则可能存在以下情形:
①FG为平行四边形的一边,且N点在x轴正半轴上,如图1所示.
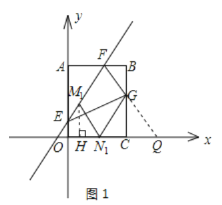
过![]() 点作
点作![]() ⊥x轴正半轴于点H,
⊥x轴正半轴于点H,
∵![]()
∴![]()
又∵AB∥OQ
∴∠HQF=∠BFG
∴![]()
又∵![]()
在△![]() 和△GBF中,
和△GBF中,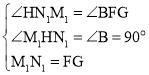
∴![]()
∴![]()
由(2)得:![]()
∴E点的坐标为![]()
设直线EF的解析式为y=kx+b,则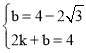
解得: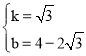
∴直线EF的解析式为![]()
∵当![]() 时,
时,![]() ,
,
∴点![]() 的坐标为
的坐标为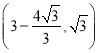
②FG为平行四边形的一边,且N点在x轴负半轴上,如图2所示.
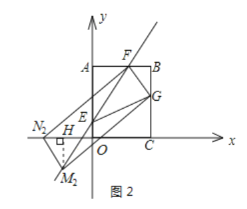
仿照与①相同的办法,可求得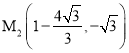
③FG为平行四边形的对角线,如图3所示.
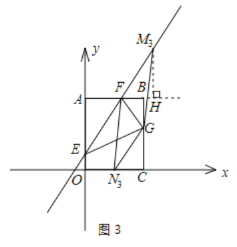
过![]() 作FB延长线的垂线,垂足为H
作FB延长线的垂线,垂足为H
则![]()
在△![]() 和△
和△![]() 中,
中,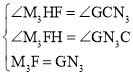
∴![]()
∴![]()
∴![]() 的纵坐标为
的纵坐标为![]()
代入直线EF解析式,得到![]() 的横坐标为
的横坐标为![]()
∴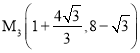
综上所述,存在点M,使以M、N、F、G为顶点的四边形是平行四边形.
点M的坐标为: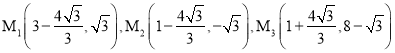


科目:初中数学 来源: 题型:
【题目】如图,钟表的分针匀速旋转一周需要60分钟,那么:
(1)它的旋转中心是什么?
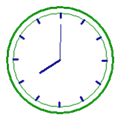
(2)分针旋转一周,时针旋转多少度?
(3)上午8点整,时针和分针的夹角是多少?8点半呢?
查看答案和解析>>
科目:初中数学 来源: 题型:
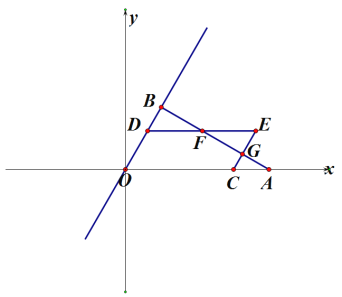
【题目】如图:在平面直角坐标系中,点A在X轴的正半轴,OA=8 ,点B在第一象限,∠AOB=60°,AB⊥OB垂足为B, 点D、C分别在边OB、OA上,且OD=AC=t,以OD、OC为边作平行四边形OCED,DE交直线AB为F,CE交直线AB为点G.
(1) 当t=2时, 则E的坐标为
(2) 若ΔDFC的面积为![]() ,求t的值。
,求t的值。
(3) 当D、 B 、G、 E四点为顶点的四边形为平行四边形时,在Y轴上存在点M,过点M作FC的平行线交直线OB为点N,若以M、 N、 F、 C为顶点的四边形也是平行四边形,则点M的坐标为 (直接写出答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】倡导健康生活,推进全民健身,某社区要购进A,B两种型号的健身器材若干套,A,B两种型号健身器材的购买单价分别为每套310元,460元,且每种型号健身器材必须整套购买.
(1)若购买A,B两种型号的健身器材共50套,且恰好支出20000元,求A,B两种型号健身器材各购买多少套?
(2)若购买A,B两种型号的健身器材共50套,且支出不超过18000元,求A种型号健身器材至少要购买多少套?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:直线AB∥CD,点E. F分别是AB、CD上的点。
(1)如图1,当点P在AB、CD内部时,试说明:∠EPF=∠AEP+∠CFP;
(2)如图2,当点P在AB上方时,∠EPF、∠AEP、∠CFP之间有怎样的数量关系?并说明理由。


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A、B在反比例函数y=![]() 的图象上,过点A、B作x轴的垂线,垂足分别是M、N,射线AB交x轴于点C,若OM=MN=NC,四边形AMNB的面积是3,则k的值为( )
的图象上,过点A、B作x轴的垂线,垂足分别是M、N,射线AB交x轴于点C,若OM=MN=NC,四边形AMNB的面积是3,则k的值为( )
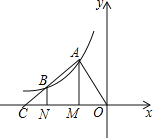
A.2 B.4 C.﹣2 D.﹣4
查看答案和解析>>
科目:初中数学 来源: 题型:
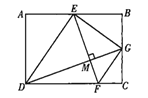
【题目】如图,点E是矩形ABCD的边AB的中点,点F是边CD上一点,连接ED,EF,ED平分∠AEF,过点D作DG⊥EF于点M,交BC于点G,连接GE,GF,若FG∥DE,则![]() 的值是( )
的值是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,物理教师为同学们演示单摆运动,单摆左右摆动中,在OA的位置时俯角∠EOA=30°,在OB的位置时俯角∠FOB=60°,若OC⊥EF,点A比点B高7cm.

(1)求单摆的长度;
(2)求从点A摆动到点B经过的路径长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com