
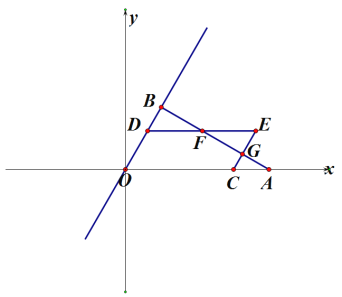
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���A��X��������ᣬOA=8 ,��B�ڵ�һ���ޣ���AOB=60�㣬AB��OB����ΪB, ��D��C�ֱ��ڱ�OB��OA�ϣ���OD=AC=t,��OD��OCΪ����ƽ���ı���OCED,DE��ֱ��ABΪF,CE��ֱ��ABΪ��G.
(1) ��t=2ʱ�� ��E������Ϊ�� ��
(2) ����DFC�����Ϊ![]() ����t��ֵ��
����t��ֵ��
(3) ��D�� B ��G�� E�ĵ�Ϊ������ı���Ϊƽ���ı���ʱ����Y���ϴ��ڵ�M,����M��FC��ƽ���߽�ֱ��OBΪ��N������M�� N�� F�� CΪ������ı���Ҳ��ƽ���ı��Σ����M������Ϊ �� ��ֱ��д���𰸣�
���𰸡���1��(7��![]() )����2��
)����2��![]() ����3����0��
����3����0��![]() ������0��
������0��![]() ��.
��.
��������
��1������ƽ���ı��ε������Լ����ɶ������㼴�ɣ�
��2�����������ε������ʽ���ú�t�Ĵ���ʽ�ֱ��ʾ�������εĵߣ��г����̼��ɣ�
��3���ȸ����ı���BDGE��ƽ���ı��μ����t��ֵ���ٸ����ı���MNCF��ƽ���ı��������M�����꼴�ɣ�
��1������D��DQ��OA�ڵ�Q����� DQO=90��
��t=2ʱ��OD=AC=2
��OC=OA-AC=8-2=6
��ƽ���ı���OCED�У�DE=OC=6
��Rt��OQD����AOB=60������ DQO=90����
��![]() ��
��![]()
���E�ĺ�����Ϊ��1+6=7��������Ϊ��![]()
�ʵ�E������Ϊ����7��![]() ��
��
��2����ƽ���ı���OCED�У�CE=OD=t����OD��CE��OC��DE
��AB��OB
��� ABO=90��
�֡�OD��CE
��� AGC=90������ACG=��AOB=60����
��Rt��ACG����ACG =60������AGC =90����
��![]() ��
��
��![]()
��CG=EG
��OC��DE
���ACG=��FEG
����ACG����FEG��
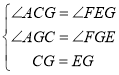
����ACG����FEG
��EF=AC=t
��![]()
�ɣ�1��֪��![]() ����
����![]()
��![]()
�֡���DFC�����Ϊ![]()
��![]()
��ã�![]() ��
��![]()
��3������M��y����������ʱ��
��Rt��AOB����AOB =60������ABO =90����
��![]() ��
��
��![]()
���ı���BDGE��ƽ���ı���
��![]()
��![]()
�ɣ�2��֪![]()
��![]()
��ã�![]()
��![]()
��OC��DE��DQ��OC��FP��OC
��![]()
���ı���MNCF��ƽ���ı��Σ�
����MN=CF
�����������ã���CPF�ա�NHM
��![]() ��
��![]()
��Rt��OHN����OHN =90������HON =90��-60��=30����
��![]() ��
��
��![]()
���M��������0��![]() ��
��
����M��y�Ḻ������ʱ��ͬ���ɵõ�M������Ϊ��0��![]() ��
��
������������M��������0��![]() ����0��
����0��![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
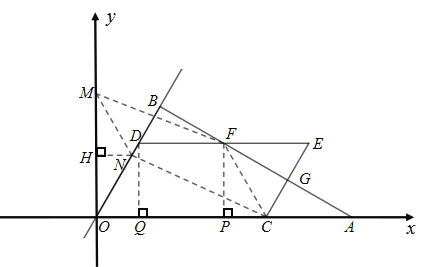
����Ŀ����ͼ����һ������������ʾ��ͼ�����MN������߶�AB��
CDΪˮƽ���ߣ������������ԭ��֪��AB��MN��CD��MN��
��1��������MN��35mm������CL��50mm������ľ���߶�AB��4.9m��������뾰��ľ���LD�Ƕ��٣�
��2�����Ҫ����������߶���2m�ľ��������뾰����4m����߲��䣬������Ľ���Ӧ����Ϊ���ٺ��ף�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˾���ʵʩ����ƶ�¸���С������ΰ��ͼ��ij�ط�ƶ������Ϊ�������幺����һ��ƻ������������磬��֪һ��ƻ�������һ���������2Ԫ������ƻ������ķ��ú���������ķ��÷ֱ���3500Ԫ��2500Ԫ��
��1�����������繺��Ŀ���һ���࣬��������ĵ��ۣ�
��2�����������繲����1100�ã��ҹ�������������ܷ��ò�����6000Ԫ�����ݣ�1������������ĵ��ۣ������������ٹ�����ٿã�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������֣�����֪������������y��![]() ��x��0����ͼ����˫���ߣ���ô����y��
��x��0����ͼ����˫���ߣ���ô����y��![]() +n��k��m��nΪ������k��0����ͼ����˫���������뷴��������y��
+n��k��m��nΪ������k��0����ͼ����˫���������뷴��������y��![]() ��x��0����ͼ���������Ĺ�ϵ�أ�������һ����̽��֮�á���
��x��0����ͼ���������Ĺ�ϵ�أ�������һ����̽��֮�á���
̽��˼�������ǿ��Խ����ǰ�о������ķ���������̽������y��![]() ��ͼ��
��ͼ��
��1����д�±�������������y��![]() ��ͼ��
��ͼ��
�����
x | �� | ��5 | ��3 | ��2 | 0 | 1 | 3 | �� |
y | �� | �� |
����㲢���ߣ�
��2���۲�ͼ��д���ú���ͼ���������ͬ���͵�������
���� ������ ����
�������ã�����y��![]() ��ͼ�����ɺ���y��
��ͼ�����ɺ���y��![]() ��ͼ������ ��ƽ���� ������λ����Գ����ĵ�����Ϊ�� ����
��ͼ������ ��ƽ���� ������λ����Գ����ĵ�����Ϊ�� ����
���Ӧ�ã���������������ͼ��ľ��飬��һ�뺯��y��![]() +2��ͼ�����λ�ã�������ͼ��ָ������x������ ��ʱ��y��3��
+2��ͼ�����λ�ã�������ͼ��ָ������x������ ��ʱ��y��3��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
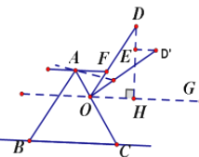
����Ŀ��ͼ 1 ��С���ڡ��Ա�˫ 11������������һ�Ŷ൵λ�ɵ��ڿ��Σ���λ����ʾ��ͼ��ͼ 2 ��ʾ����֪��֧�� AB=AC��O Ϊ AC �Ϲ̶����ӵ㣬���� OD=10 ���ס���λΪ��ʱ��OD��AB����λΪ��ʱ��OD����AC,����O��OG��BC,���DOG+��D��OG=_________�㵱�����ɢ���Ϊ��ʱ���������� D ����� D������ʱ�� D �ƶ���ˮƽ������ 2 ���ף��� ED��=2 ���ס�DH��OG�ڵ�H����D��ֱ��OG�ľ���Ϊ_________ ����.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪![]() �Ľ�����������������
�Ľ�����������������![]() ����
����![]() ��
��![]() ����
����![]() ����
����![]() ��
��![]() ������һ������ֱ�������ε���______.��ֻ����ţ�
������һ������ֱ�������ε���______.��ֻ����ţ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����![]() ABCD�У� �Խ���AC��BD�ཻ�ڵ�O. E��F�ǶԽ���AC�ϵ�������ͬ�㣬��E��F����������������ʱ���ı���DEBF��һ����ƽ���ı���( ).
ABCD�У� �Խ���AC��BD�ཻ�ڵ�O. E��F�ǶԽ���AC�ϵ�������ͬ�㣬��E��F����������������ʱ���ı���DEBF��һ����ƽ���ı���( ).

A.AE��CFB.DE��BFC.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı���ABCDΪ�����Σ�C����x�ᣬA����y���ϣ�D��������(0��0)��B��������(3��4)��������ABCD��ֱ��EF�۵�����A����BC���ϵ�G����E��F�ֱ���AD��AB�ϣ�F(2��4)��
��1����G�����ꣻ
��2����EFG�����Ϊ�� ����ֱ����գ���
��3����N��x���ϣ�ֱ��EF���Ƿ���ڵ�M��ʹ��M��N��F��GΪ������ı�����ƽ���ı��Σ������ڣ���ֱ��д��M��������ꣻ�������ڣ���˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼͼ������ͬ����С��ͭ�Ұڷŵ��ĸ�ͼ�������ݰڷ�ͼ���Ĺ��ɣ����8��ͼ����Ҫͭ�ҵĸ���Ϊ��������

A.29B.36C.37D.46
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com