
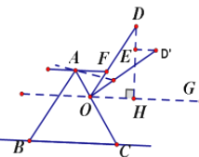
【题目】图 1 是小红在“淘宝双 11”活动中所购买的一张多档位可调节靠椅,档位调节示意图如图 2 所示。已知两支脚 AB=AC,O 为 AC 上固定连接点,靠背 OD=10 分米。档位为Ⅰ档时,OD∥AB,档位为Ⅱ挡时,OD’⊥AC,过点O作OG∥BC,则∠DOG+∠D’OG=_________°当靠椅由Ⅰ档调节为Ⅱ档时,靠背顶端 D 向后靠至 D’,此时点 D 移动的水平距离是 2 分米,即 ED’=2 分米。DH⊥OG于点H,则D到直线OG的距离为_________ 分米.

【答案】90 8
【解析】
先利用平行线的性质与等腰三角形的性质证明∠DOG=∠COG,在利用等量代换计算出∠DOG+∠D’OG=∠COD’=90°;先构造Rt△OMD’,再利用全等的性质以及勾股定理计算DH的长.
(1)过点D’作MD’⊥OH于点M,记AB与OH交于点N
∵OD∥AB,OG∥BC
∴∠DOG=∠ANO,∠ANO=∠ABC,∠ACB=∠COG
∴∠DOG=∠ABC
∵AB=AC
∴∠ABC=∠ACB
∴∠DOG=∠ABC=∠ACB=∠COG
∵OD’⊥AC
∴∠COD’=90°
∴∠DOG+∠D’OG=∠COG+∠D’OG=∠COD’=90°
(2)∵DH⊥OG,D’M⊥OG
∴∠OHD=∠OMD’=90°
∴在Rt△OHD中,∠DOG+∠ODH=90°
又∵∠DOG+∠D’OG=90°
∴∠ODH=∠D’OG
∵旋转
∴OD=D’O
在△ODH和△D’OM中

∴△ODH≌△D’OM(AAS)
∴DH=OM
又∵HM=ED’=2
∴DH=OM=OH+HM=OH+2
不妨设OH=x,则DH=x+2
∴在Rt△OHD中,OD=10,
由勾股定理可得:![]()
即:![]()
解得:![]() ,
,![]() (舍去)
(舍去)
∴D到直线OG的距离为DH=x+2=8.
故答案为:90,8.



 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案科目:初中数学 来源: 题型:
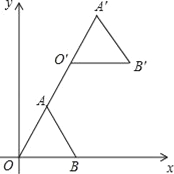
【题目】如图,在平面直角坐标系中,正三角形OAB的顶点B的坐标为(2,0),点A在第一象限内,将△OAB沿直线OA的方向平移至△O′A′B′的位置,此时点A′的横坐标为3,则点B′的坐标为( )
A. (4,2![]() ) B. (3,3
) B. (3,3![]() ) C. (4,3
) C. (4,3![]() ) D. (3,2
) D. (3,2![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
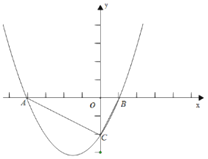
【题目】如图,已知抛物线![]() 轴交于点A(-4,0)和B(1,0)两点,与y轴交于C点.
轴交于点A(-4,0)和B(1,0)两点,与y轴交于C点.
(1)求此抛物线的解析式;
(2)设E是线段AB上的动点,作EF∥AC交BC于F,连接CE,当△CEF的面积是△BEF面积的2倍时,求E点的坐标;
(3)若P为抛物线上A、C两点间的一个动点,过P作y轴的平行线,交AC于Q,当P点运动到什么位置时,线段PQ的值最大,并求此时P点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了尽快实施“脱贫致富奔小康”宏伟意图,某县扶贫工作队为朝阳沟村购买了一批苹果树苗和梨树苗,已知一棵苹果树苗比一棵梨树苗贵2元,购买苹果树苗的费用和购买梨树苗的费用分别是3500元和2500元.
(1)若两种树苗购买的棵数一样多,求梨树苗的单价;
(2)若两种树苗共购买1100棵,且购买两种树苗的总费用不超过6000元,根据(1)中两种树苗的单价,求梨树苗至少购买多少棵.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于
轴分别交于![]() 两点,
两点,![]() 于点
于点![]() ,点
,点![]() 为直线
为直线![]() 上不与点
上不与点![]() 重合的一个动点.
重合的一个动点.
(1)求线段![]() 的长;
的长;
(2)当![]() 的面积是6时,求点
的面积是6时,求点![]() 的坐标;
的坐标;
(3)在![]() 轴上是否存在点
轴上是否存在点![]() ,使得以
,使得以![]() 、
、![]() 、
、![]() 为顶点的三角形与
为顶点的三角形与![]() 全等,若存在,请直接写出所有符合条件的点
全等,若存在,请直接写出所有符合条件的点![]() 的坐标,否则,说明理由.
的坐标,否则,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
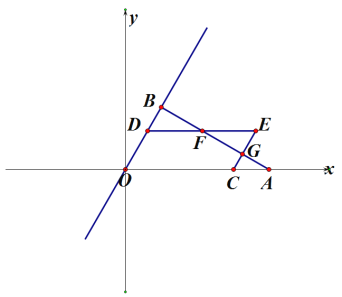
【题目】如图:在平面直角坐标系中,点A在X轴的正半轴,OA=8 ,点B在第一象限,∠AOB=60°,AB⊥OB垂足为B, 点D、C分别在边OB、OA上,且OD=AC=t,以OD、OC为边作平行四边形OCED,DE交直线AB为F,CE交直线AB为点G.
(1) 当t=2时, 则E的坐标为
(2) 若ΔDFC的面积为![]() ,求t的值。
,求t的值。
(3) 当D、 B 、G、 E四点为顶点的四边形为平行四边形时,在Y轴上存在点M,过点M作FC的平行线交直线OB为点N,若以M、 N、 F、 C为顶点的四边形也是平行四边形,则点M的坐标为 (直接写出答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A![]() ,B(-1,2)是一次函数
,B(-1,2)是一次函数![]() 与反比例函数
与反比例函数![]()
(![]() )图象的两个交点,AC⊥x轴于C,BD⊥y轴于D.
)图象的两个交点,AC⊥x轴于C,BD⊥y轴于D.
(1)根据图象直接回答:在第二象限内,当x取何值时,一次函数大于反比例函数的值?
(2)求一次函数解析式及m的值;
(3)P是线段AB上的一点,连接PC,PD,若△PCA和△PDB面积相等,求点P坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:直线AB∥CD,点E. F分别是AB、CD上的点。
(1)如图1,当点P在AB、CD内部时,试说明:∠EPF=∠AEP+∠CFP;
(2)如图2,当点P在AB上方时,∠EPF、∠AEP、∠CFP之间有怎样的数量关系?并说明理由。


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 与x轴、y轴分别交于点B、点C,经过B、C两点的抛物线
与x轴、y轴分别交于点B、点C,经过B、C两点的抛物线![]() 与x轴的另一个交点为A,顶点为P.
与x轴的另一个交点为A,顶点为P.

(1)求该抛物线的解析式;
(2)连接AC,在x轴上是否存在点Q,使以P、B、Q为顶点的三角形与△ABC相似?若存在,请求出点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com