
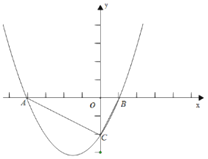
【题目】如图,已知抛物线![]() 轴交于点A(-4,0)和B(1,0)两点,与y轴交于C点.
轴交于点A(-4,0)和B(1,0)两点,与y轴交于C点.
(1)求此抛物线的解析式;
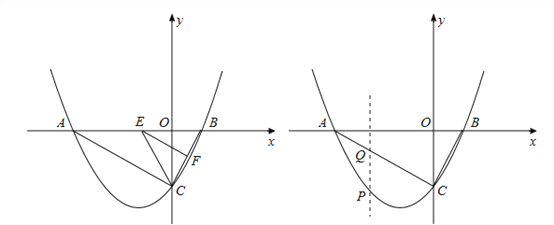
(2)设E是线段AB上的动点,作EF∥AC交BC于F,连接CE,当△CEF的面积是△BEF面积的2倍时,求E点的坐标;
(3)若P为抛物线上A、C两点间的一个动点,过P作y轴的平行线,交AC于Q,当P点运动到什么位置时,线段PQ的值最大,并求此时P点的坐标.
【答案】(1)![]() ;(2)E的坐标是
;(2)E的坐标是![]() ; (3)P点的坐标是(-2,-3).
; (3)P点的坐标是(-2,-3).
【解析】试题分析:(1)将A、B的坐标代入抛物线的解析式中,即可求出待定系数的值;
(2)根据抛物线的解析式可得出C点的坐标,易证得△ABC是直角三角形,则EF⊥BC;△CEF和△BEF同高,则面积比等于底边比,由此可得出CF=2BF;易证得△BEF∽△BAC,根据相似三角形的性质,即可求得BE、AB的比例关系,由此可求出E点坐标;
(3)PQ的长实际是直线AC与抛物线的函数值的差,可设P点横坐标为m,用m表示出P、Q的纵坐标,然后可得出PQ的长与m的函数关系式,根据所得函数的性质即可求出PQ最大时,m的值,也就能求出此时P点的坐标.
试题解析:解:(1)由题意得: 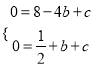 ,解得:
,解得: 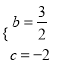 ,∴
,∴![]() ;
;
(2)由(1)知:C(0,﹣2),则AC2=AO2+OC2=20,BC2=BO2+OC2=5.
而AB2=25=AC2+BC2,∴△ACB是直角三角形,且∠ACB=90°,∴AC⊥BC,∵EF∥AC,∴EF⊥BC.∵S△CEF=2S△BEF,∴CF=2BF,BC=3BF.∵EF∥AC,∴ ![]() .
.
∵AB=5,∴BE=![]() ,OE=BE﹣OB=
,OE=BE﹣OB=![]() ,故E(
,故E(![]() ,0);
,0);
(3)设P点坐标为(m, ![]() ).已知A(﹣4,0),C(0,﹣2),设直线AC的解析式为:y=kx﹣2,则有:﹣4k﹣2=0,∴k=﹣
).已知A(﹣4,0),C(0,﹣2),设直线AC的解析式为:y=kx﹣2,则有:﹣4k﹣2=0,∴k=﹣![]() ,∴直线AC的解析式为y=﹣
,∴直线AC的解析式为y=﹣![]() x﹣2,
x﹣2,
∴Q点坐标为(m,﹣ ![]() m﹣2),则PQ=(﹣
m﹣2),则PQ=(﹣![]() m﹣2)﹣(
m﹣2)﹣(![]() )=﹣
)=﹣![]() m2﹣2m=
m2﹣2m=![]() ,∴当m=﹣2,即P(﹣2,﹣3)时,PQ最大,且最大值为2.
,∴当m=﹣2,即P(﹣2,﹣3)时,PQ最大,且最大值为2.
故当P运动到OA垂直平分线上时,PQ的值最大,此时P(﹣2,﹣3).


 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案科目:初中数学 来源: 题型:
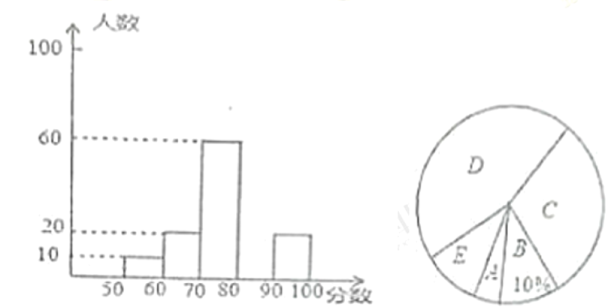
【题目】七年级数学研究学习小组在某↑字路口随机调查部分市民对“社会主义核心价值观”的了解情况,统计结果后绘制了如图的两副不完整的统计图,请结合图中相关数据回答下列问题:
得分 | |
|
|
|
|
|
|
|
|
|
|
(1)本次调查的总人数为 人, 在扇形统计图中“心所在扇形的圆心角的度数为 :
(2)补全频数分布图:
(3)若在这周里,该路口共有![]() 人通过,请估计得分超过
人通过,请估计得分超过![]() 的约有多少人?
的约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示的曲线是函数y=![]() (m为常数)图象的一支.
(m为常数)图象的一支.
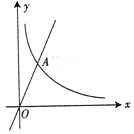
(1)求常数m的取值范围;
(2)若该函数的图象与正比例函数y=2x的图象在第一象限的交点为A(2,n),求点A的坐标及反比例
函数的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
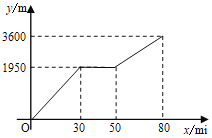
【题目】小颖和小亮上山游玩,小颖乘会缆车,小亮步行,两人相约在山顶的缆车终点会合.已知小亮行走到缆车终点的路程是缆车到山顶的线路长的2倍,小颖在小亮出发后50 min才乘上缆车,缆车的平均速度为180 m/min.设小亮出发x min后行走的路程为y m.图中的折线表示小亮在整个行走过程中y与x的函数关系.
⑴小亮行走的总路程是____________cm,他途中休息了________min.
⑵①当50≤x≤80时,求y与x的函数关系式;
②当小颖到达缆车终点为时,小亮离缆车终点的路程是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,用相同的小正方形按照某种规律进行摆放.根据图中小正方形的排列规律,猜想第![]() 个图中小正方形的个数为___________(用含
个图中小正方形的个数为___________(用含![]() 的式子表示)
的式子表示)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了尽快实施“脱贫致富奔小康”宏伟意图,某县扶贫工作队为朝阳沟村购买了一批苹果树苗和梨树苗,已知一棵苹果树苗比一棵梨树苗贵2元,购买苹果树苗的费用和购买梨树苗的费用分别是3500元和2500元.
(1)若两种树苗购买的棵数一样多,求梨树苗的单价;
(2)若两种树苗共购买1100棵,且购买两种树苗的总费用不超过6000元,根据(1)中两种树苗的单价,求梨树苗至少购买多少棵.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线![]() 经过点
经过点![]() 和
和![]() ,分别与x轴、y轴交于A、B两点.
,分别与x轴、y轴交于A、B两点.
(1)求直线![]() 的解析式:
的解析式:
(2)若把横、纵坐标均为整数的点称为格点,则图中阴影部分(不包括边界)所含格点的个数有 个;
(3)作出点![]() 关于直线
关于直线![]() 的对称点
的对称点![]() ,则点
,则点![]() 的坐标为 ;
的坐标为 ;![]()
(4)若在直线![]() 和
和![]() 轴上分别存在一点
轴上分别存在一点![]() 使
使![]() 的周长最短,请在图中标出点
的周长最短,请在图中标出点![]() (不写作法,保留痕迹).
(不写作法,保留痕迹).

查看答案和解析>>
科目:初中数学 来源: 题型:
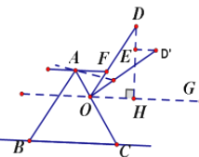
【题目】图 1 是小红在“淘宝双 11”活动中所购买的一张多档位可调节靠椅,档位调节示意图如图 2 所示。已知两支脚 AB=AC,O 为 AC 上固定连接点,靠背 OD=10 分米。档位为Ⅰ档时,OD∥AB,档位为Ⅱ挡时,OD’⊥AC,过点O作OG∥BC,则∠DOG+∠D’OG=_________°当靠椅由Ⅰ档调节为Ⅱ档时,靠背顶端 D 向后靠至 D’,此时点 D 移动的水平距离是 2 分米,即 ED’=2 分米。DH⊥OG于点H,则D到直线OG的距离为_________ 分米.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学为打造书香校园,计划购进甲、乙两种规格的书柜放置新购进的图书,调查发现,若购买甲种书柜![]() 个、乙种书柜
个、乙种书柜![]() 个,共需资金
个,共需资金![]() 元;若购买甲种书柜
元;若购买甲种书柜![]() 个,乙种书柜
个,乙种书柜![]() 个,共需资金
个,共需资金![]() 元
元
(1)甲、乙两种书柜每个的价格分别是多少元?
(2)若该校计划购进这两种规格的书柜共![]() 个,学校至多能够提供资金
个,学校至多能够提供资金![]() 元,请设计几种购买方案供这个学校选择.(两种规格的书柜都必须购买)
元,请设计几种购买方案供这个学校选择.(两种规格的书柜都必须购买)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com