
【题目】阅读下面的材料:
点A、B在数轴上分别表示实数a,b,A,B两点之间的距离表示为|AB|
当A、B两点中有一点在原点时,设点A在原点,如图①|AB|=|OB|=|b|=|a﹣b|
当A、B两点都不在原点时,

(1)如图②,点A,B都在原点的右边,|AB|=|OB|﹣|OA|=|b|﹣|a|=b﹣a=|a﹣b|
(2)如图③,点A、B都在原点的左边,|AB|=|OB|﹣|OA|=|b|﹣|a|=﹣b﹣(﹣a)=|a﹣b|
(3)如图④,点A、B在原点的两边,|AB|=|OA|+|OB|=|a|+|b|=a+(﹣b)=|a﹣b|
综上所述,数轴上A、B两点之间的距离|AB|=|a﹣b|
请用上面的知识解答下面的问题:
(1)数轴上表示﹣2和﹣4的两点之间的距离是 ,数轴上表示1和﹣3的两点之间的距离是 .
(2)数轴上表示x和﹣1的两点A和B之间的距离是 ,如果|AB|=2,那么x为 .
(3)当|x+1|+|x﹣2|=5时的整数x的值 .
(4)当|x+1|+|x﹣2|取最小值时,相应的x的取值范围是 .
【答案】(1)2 4;(2)|x+1| 1或-3;(3)-2或3;(4)-1≤ x≤2.
【解析】
(1)(2)直接根据数轴上A、B两点之间的距离|AB|=|a﹣b|.代入数值运用绝对值即可求任意两点间的距离;
(3)根据题意分三种情况:当x≤﹣1时,当﹣1<x≤2时,当x>2时,分别求出方程的解即可;
(4)根据绝对值的性质,可得到一个一元一次不等式组,通过求解,就可得出x的取值范围.
(1)数轴上表示﹣2和﹣4的两点之间的距离是|﹣2﹣(﹣4)|=2;
数轴上表示1和﹣3的两点之间的距离是|1﹣(﹣3)|=4
故答案为:2,4
(2)数轴上x与-1的两点间的距离为|x-(-1)|=|x+1|,如果|AB|=2,则x+1=±2,解得x=1或-3;
故答案为:|x+1|,1或-3
(3)解方程|x+1|+|x﹣2|=5,且x为整数.
当x+1>0,x-2>0,则(x+1)+(x-2)=5,解得x=3
当x+1<0,x-2<0,则-(x+1)-(x-2)=5,解得x=-2
当x+1与x-2异号,则等式不成立.
所以答案为:3或-2.
(4)根据题意得x+1≥0且x-2≤0,则-1≤x≤2;


 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案科目:初中数学 来源: 题型:
【题目】如图所示,把一根绳子对折后得到的图形为线段AB,从点P处把绳子剪断,已知AP:BP=4:5,若剪断后的各段绳子中最长的一段为80cm,则绳子的原长为________ cm.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,C是AB的中点,D是BE的中点,

(1)AB=4cm,BE=3cm,则CD=____________cm;
(2)AB=4cm,DE=2cm,则AE=____________cm;
(3)AB=4cm,BE=2cm,则AD=____________cm;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】绿水青山就是金山银山,国家倡导全民植树。在今年3月12日植树节当天,某校七年级一班48名学生全部参加了植树活动,男生每人栽种4株,女生每人栽种3株,全班共栽种170株。
(1)该班男、女生各为多少人?
(2)学校选择购买甲、乙两种树苗,甲树苗![]() ,乙树苗
,乙树苗![]() .如果要使购买树苗的钱不超过1200元,那么最多可以购买甲树苗多少株?
.如果要使购买树苗的钱不超过1200元,那么最多可以购买甲树苗多少株?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,AD平分∠CAB,交CB于点D,过点D作DE⊥AB,于点E
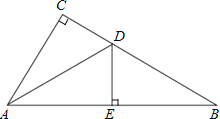
(1)求证:△ACD≌△AED;
(2)若∠B=30°,CD=1,求BD的长。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AO为Rt△ABC的角平分线,∠ACB=90°,![]() ,以O为圆心,OC 为半径的圆分别交AO,BC于点D,E,连接ED并延长交AC于点F.
,以O为圆心,OC 为半径的圆分别交AO,BC于点D,E,连接ED并延长交AC于点F.
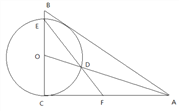
(1)求证:AB是⊙O的切线;
(2)求![]() 的值。
的值。
(3)若⊙O的半径为4,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知如图,点 C 在以 AB 为直径的⊙O 上,点 D 在 AB 的延长线上,∠BCD =∠A.
(1)求证:CD 为⊙O 的切线;
(2)过点 C 作 CE⊥AB 于点 E.若 CE = 2,cos D =![]() ,求 AD 的长.
,求 AD 的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知x1,x2是一元二次方程(a﹣6)x2+2ax+a=0的两个实数根.
(1)是否存在实数a,使﹣x1+x1x2=4+x2成立?若存在,求出a的值;若不存在,请你说明理由;
(2)求使(x1+1)(x2+1)为正整数的实数a的整数值.
查看答案和解析>>
科目:初中数学 来源: 题型:
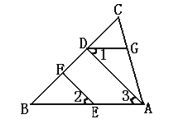
【题目】如图,EF∥AD,∠1=∠2,∠BAC=72 o,求∠AGD的度数.
解:因为EF∥AD
所以∠2= ( )
又因为∠1=∠2
所以∠1=∠3
所以AB∥ ( )
所以∠BAC+ =180 o( )
因为∠BAC=72 o
所以∠AGD= ( )
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com