练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    在△ABC中，如果AB=AC=5cm，BC=8cm，那么这个三角形的重心G到BC的距离是__________cm．


    1cm．

    【考点】勾股定理；三角形的重心；等腰三角形的性质．

    【分析】根据等腰三角形的三线合一，知三角形的重心在BC边的高上．根据勾股定理求得该高，再根据三角形的重心到顶点的距离是它到对边中点的距离的2倍，求得G到BC的距离．

    【解答】解：∵AB=AC=5cm

    ∴△ABC是等腰三角形

    ∴三角形的重心G在BC边的高

    根据勾股定理设该高为a，

    ∴a2+42=52

    则a=3cm，

    根据三角形的重心性质

    ∴G到BC的距离是1cm．

    【点评】考查了等腰三角形的三线合一的性质以及三角形的重心的概念和性质．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


    ．阅读下面材料：

    一个含有多个字母的式子中，如果任意交换两个字母的位置，式子的值都不变，这样的式子就叫做对称式. 例如：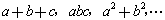

    含有两个字母a，b的对称式的基本对称式是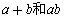，像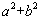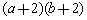， 等对称式都可以用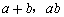表示，例如：.

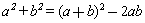    请根据以上材料解决下列问题：

    （1）式子① 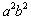  ②  ③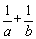中，属于对称式的是_________(填序号)；

    （2）已知 .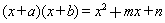

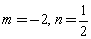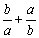    ①若，求对称式的值；

    ②若，直接写出对称式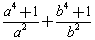的最小值.

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    请任意写出一个无理数：      ．

      

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    一件衬衫先按成本加价60元标价，再以8折出售，仍可获利24元，这件衬衫的成本是

             多少钱？设衬衫的成本为x元.

            （1）填写下表：（用含有x的代数式表示）

    成本

    标价

    售价

    x

            （2）根据相等关系列出方程：       

           .

      

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如果3x=2y，那么=__________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    已知平行四边形ABCD的对角线AC与BD相交于点O，设=，=，则向量关于、的分解式为__________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


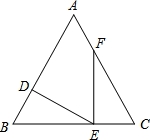
    在△ABC中，AB=AC=5，BC=6，点D在边AB上，DE⊥AB，点E在边BC，点F在边AC上，且∠DEF=∠B．

    （1）求证：△FCE∽△EBD；

    （2）当点D在线段AB上运动时，是否有可能使S△FCE=4S△EBD？如果有可能，那么求出BD的长；如果不可能，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


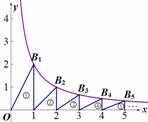
    如图，已知反比例函数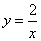的图象上有一组点B1，B2，…，Bn，它们的横坐标依次增加1，且点B1横坐标为1．“①，②，③…”分别表示如图所示的三角形的面积，记S1=①-②，S2=②-③，…，则S7的值为           ，S1+S2+…+Sn=                     （用含n的式子表示）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    在矩形ABCD中，边AD=8，将矩形ABCD折叠，使得点B落在CD边上的点P处（如图1）．

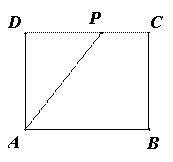
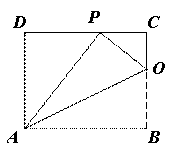
    图1                         图2

    （1）如图2，设折痕与边BC交于点O，连接,OP、OA．已知△OCP与△PDA的面积比为1：4，求边AB的长；

    （2）动点M在线段AP上（不与点P、A重合），动点N在线段AB的延长线上，且BN=PM，连接MN、 PA，交于点F，过点M作ME⊥BP于点E．

    ①在图1中画出图形；

    ②在△OCP与△PDA的面积比为1：4不变的情况下，试问动点M、N在移动的过程中，线段EF的长度是否发生变化？请你说明理由．

    查看答案和解析>>

    同步练习册答案