
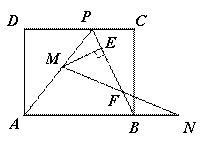
在矩形ABCD中,边AD=8,将矩形ABCD折叠,使得点B落在CD边上的点P处(如图1).
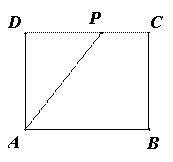
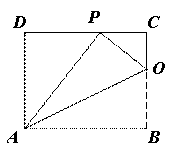
图1 图2
(1)如图2,设折痕与边BC交于点O,连接,OP、OA.已知△OCP与△PDA的面积比为1:4,求边AB的长;
(2)动点M在线段AP上(不与点P、A重合),动点N在线段AB的延长线上,且BN=PM,连接MN、 PA,交于点F,过点M作ME⊥BP于点E.
①在图1中画出图形;
②在△OCP与△PDA的面积比为1:4不变的情况下,试问动点M、N在移动的过程中,线段EF的长度是否发生变化?请你说明理由.
解:(1)如图2,∵四边形ABCD是矩形,
∴∠C=∠D=90°.
 ∴∠1+∠3=90°.
∴∠1+∠3=90°.
∵由折叠可得∠APO=∠B=90°,
∴∠1+∠2=90°.
∴∠2=∠3.-------------------------1分
又∵∠D=∠C, 2
∴△OCP∽△PDA.---------------------------------------------2分
如图1,∵△OCP与△PDA的面积比为1:4,
∴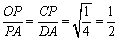 .∴CP=
.∴CP=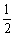 AD=4.
AD=4.
设OP=x,则CO=8-x.
在Rt△PCO中,∠C=90°,
由勾股定理得 x2=(8-x)2+42.---------------------------------------------3分
解得:x=5.
∴AB=AP=2OP=10. -------------------------------------------------4分
∴边AB的长为10.
 (2)①----------5分
(2)①----------5分
②在△OCP与△PDA的面积比为1:4这一条件不变的情况下,点M、N在移动过程中,线段EF的长度是不变的.
过点M作MQ∥AN,交PB于点Q,如图.
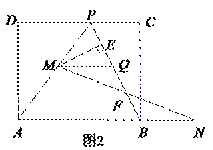 ∵AP=AB,MQ∥AN,
∵AP=AB,MQ∥AN,
∴∠APB=∠ABP=∠MQP.
∴MP=MQ.又ME⊥PQ
∴点E是PQ的中点
∵MP=MQ,BN=PM,,.
∴BN=QM,又 MQ∥AN
可证点F是QB的中点
∴EF=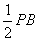 . ------------------------------------------------6分
. ------------------------------------------------6分
∵△BCP中,∠C=90°,PC=4,BC=AD=8
∴PB=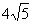 为定值
为定值
∴EF为定值. ----------------------------------------------------------7分
∴在△OCP与△PDA的面积比为1:4这一条件不变的情况下,点M、N在移动过程中,线段EF的长度是不变的它的.


 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案科目:初中数学 来源: 题型:
如图①,在平面直角坐标系中,直径为 的⊙A经过坐标系原点O(0,0),与x轴交于点B,与y轴交于点C(0,
的⊙A经过坐标系原点O(0,0),与x轴交于点B,与y轴交于点C(0,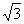 ).
).
(1)求点B的坐标;
(2)如图②,过点B作⊙A的切线交直线OA于点P,求点P的坐标;
(3)过点P作⊙A的另一条切线PE,请直接写出切点E的坐标.
|
|
|
| 图① | 图② |
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC(顶点是网格线的交点).
(1)将△ABC绕点B顺时针旋转90°得到△A’BC ’,请画
出△A’BC ’,并求BA边旋转到B A’’位置时所扫过图形的面积;
(2)请在网格中画出一个格点△A”B”C”,使△A”B”C”∽△ABC,
且相似比不为1.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com