【题目】张师傅开车到某地送货，汽车出发前油箱中有油50升，行驶一段时间，张师傅在加油站加油，然后继续向目的地行驶．已知加油前、后汽车都匀速行驶，汽车行驶时每小时的耗油量一定．油箱中剩余油量Q（升）与汽车行驶时间t（时）之间的函数图象如图所示．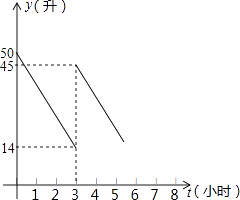

（1）张师傅开车行驶小时后开始加油，本次加油升．
（2）求加油前Q与t之间的函数关系式．
（3）如果加油站距目的地210千米，汽车行驶速度为70千米/时，张师傅要想到达目的地，油箱中的油是否够用？请通过计算说明理由．

参考答案：

【答案】
（1）3,31
（2）解：设加油前Q与t之间的函数关系式为Q=kt+b（k≠0），

将（0，50）、（3，14）代入Q=kt+b，

得： ，

解得： ，

加油前Q与t之间的函数关系式为Q=﹣12t+50（0≤t≤3）


（3）解：该车每小时耗油量为：（50﹣14）÷3=12（升），

∴到达目的地还需耗用12×（210÷70）=36（升），

∵45＞36，

∴张师傅要想到达目的地，油箱中的油够用


【解析】解：（1）观察函数图象可知：张师傅开车行驶3小时后开始加油，

45﹣14=31（升）．

所以答案是：3；31．

关闭