
【题目】如图,抛物线![]() 的图象与x轴交于A(﹣1.0),B(3,0)两点,与y轴交于点C(0,﹣3),顶点为D.
的图象与x轴交于A(﹣1.0),B(3,0)两点,与y轴交于点C(0,﹣3),顶点为D.
(1)求此抛物线的解析式.
(2)求此抛物线顶点D的坐标和对称轴.
(3)探究对称轴上是否存在一点P,使得以点P、D、A为顶点的三角形是等腰三角形?若存在,请求出所有符合条件的P点的坐标,若不存在,请说明理由.

【答案】(1)![]() ;(2)D的坐标是(1,﹣4),对称轴是直线x=1;(3)P(1,
;(2)D的坐标是(1,﹣4),对称轴是直线x=1;(3)P(1,![]() )或(1,
)或(1,![]() )或(1,
)或(1,![]() )或(1,4).
)或(1,4).
【解析】
试题分析:(1)根据抛物线![]() 的图象与x轴交于A(﹣1.0),B(3,0)两点,与y轴交于点C(0,﹣3),可以求得抛物线的解析式;
的图象与x轴交于A(﹣1.0),B(3,0)两点,与y轴交于点C(0,﹣3),可以求得抛物线的解析式;
(2)根据(1)中的解析式化为顶点式,即可得到此抛物线顶点D的坐标和对称轴;
(3)首先写出存在,然后运用分类讨论的数学思想分别求出各种情况下点P的坐标即可.
试题解析:(1)∵抛物线![]() 的图象与x轴交于A(﹣1.0),B(3,0)两点,与y轴交于点C(0,﹣3),∴
的图象与x轴交于A(﹣1.0),B(3,0)两点,与y轴交于点C(0,﹣3),∴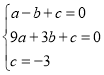 ,解得:
,解得: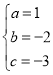 ,即此抛物线的解析式是
,即此抛物线的解析式是![]() ;
;
(2)∵![]() =
=![]() ,∴此抛物线顶点D的坐标是(1,﹣4),对称轴是直线x=1;
,∴此抛物线顶点D的坐标是(1,﹣4),对称轴是直线x=1;
(3)存在一点P,使得以点P、D、A为顶点的三角形是等腰三角形,设点P的坐标为(1,y),分三种情况讨论:
①当PA=PD时![]() =
=![]() ,解得,y=
,解得,y=![]() ,即点P的坐标为(1,
,即点P的坐标为(1,![]() );
);
②当DA=DP时,![]() =
=![]() ,解得,y=
,解得,y=![]() ,即点P的坐标为(1,
,即点P的坐标为(1,![]() )或(1,
)或(1,![]() );
);
③当AD=AP时,![]() =
=![]() ,解得,y=±4,即点P的坐标是(1,4)或(1,﹣4),当点P为(1,﹣4)时与点D重合,故不符合题意.
,解得,y=±4,即点P的坐标是(1,4)或(1,﹣4),当点P为(1,﹣4)时与点D重合,故不符合题意.
由上可得,以点P、D、A为顶点的三角形是等腰三角形时,点P的坐标为(1,![]() )或(1,
)或(1,![]() )或(1,
)或(1,![]() )或(1,4).
)或(1,4).


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】ABCD中,E是CD边上一点,
(1)将△ADE绕点A按顺时针方向旋转,使AD、AB重合,得到△ABF,如图1所示.观察可知:与DE相等的线段是 ,∠AFB=∠
(2)如图2,正方形ABCD中,P、Q分别是BC、CD边上的点,且∠PAQ=45°,试通过旋转的方式说明:DQ+BP=PQ;
(3)在(2)题中,连接BD分别交AP、AQ于M、N,你还能用旋转的思想说明BM2+DN2=MN2吗?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,为美化校园环境,某校计划在一块长为60米,宽为40米的长方形空地上修建一个长方形花圃,并将花圃四周余下的空地修建成同样宽的通道,设通道宽为![]() 米.
米.
(1)花圃的面积为____![]() (用含
(用含![]() 的式子表示);
的式子表示);
(2)如果通道所占面积是整个长方形空地面积的![]() ,求出此时通道的宽;
,求出此时通道的宽;
(3)已知某园林公司修建通道、花圃的造价![]() (元)、
(元)、![]() (元)与修建面积
(元)与修建面积![]()
![]() 之间的函数关系如图2所示,如果学校决定由该公司承建此项目,并要求修建的通道的宽度不少于2米且不超过10米,那么通道宽为多少时,修建的通道和花圃的总造价为105920元
之间的函数关系如图2所示,如果学校决定由该公司承建此项目,并要求修建的通道的宽度不少于2米且不超过10米,那么通道宽为多少时,修建的通道和花圃的总造价为105920元

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某家庭农场要建一个长方形的养兔场,兔场的两边靠墙(两堵墙互相垂直,长度不限),另两边用木栏围成,木栏总长20米.
(1)兔场的面积能达到100平方米吗?请你给出设计方案;
(2)兔场的面积能达到110平方米吗?如能,请给出设计方案,若不能说明理.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.
(1)求证:△ADF∽△DEC
(2)若AB=4,AD=3![]() ,AE=3,求AF的长.
,AE=3,求AF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】宁波某企业新增了一个化工项目,为了节约资源,保护环境,该企业决定购买A、B两种型号的污水处理设备共10台,具体情况如下表:
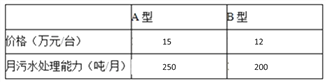
经预算,企业最多支出136万元购买设备,且要求月处理污水能力不低于2150吨.
(1)该企业有哪几种购买方案?
(2)哪种方案更省钱?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解上一次八年级数学测验成绩情况,随机抽取了40名学生的成绩进行统计分析,这40名学生的成绩数据如下:
55 62 67 53 58 83 87 64 68 85
60 94 81 98 51 83 78 77 66 71
91 72 63 75 88 73 52 71 79 63
74 67 78 61 97 76 72 77 79 71
(1)将样本数据适当分组,制作频数分布表:
分 组 |
|
|
|
|
|
频 数 |
|
|
|
|
|
(2)根据频数分布表,绘制频数直方图:
(3)从图可以看出,这40名学生的成绩都分布在什么范围内?分数在哪个范围的人数最多?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com