练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】直线y＝3x＋9与x轴的交点坐标是( )

    A. (3，0) B. (－3，0)

    C. (0，3) D. (0，－3)

    【答案】B

    【解析】直线y＝3x＋9与x轴的交点纵坐标等于0，所以令3x＋9=0，解得的x的值是即是与x轴交点的横坐标.

    由题意得，

    3x＋9=0，

    ∴x=-3，

    ∴与x轴的交点坐标是(－3，0).

    故选B.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】先化简，再求值：2（x2y+xy2）﹣2（x2y﹣x）﹣2xy2﹣2y，其中x=﹣2，y=2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】两组邻边分别相等的四边形叫做“筝形”，如图，四边形ABCD是一个筝形，其中AD=CD，AB=CB，在探究筝形的性质时，得到如下结论：①△ABD≌△CBD；②AC⊥BD；③四边形ABCD的面积= ACBD，其中正确的结论有（ ）

    A.0个
    B.1个
    C.．2个
    D.．3个

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】要得到函数y＝x2的图象只要把函数y＝(x﹣3)2的图象（　　）

    A.向左平移3个单位B.向右平移3个单位

    C.向上平移3个单位D.向下平移3个单位

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某射击运动员在相同条件下的射击160次，其成绩记录如下：

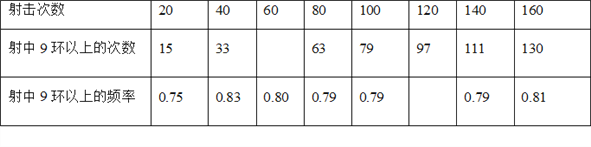
    （1）根据上表中的信息将两个空格的数据补全（射中9环以上的次数为整数，频率精确到0.01）；

    （2）根据频率的稳定性，估计这名运动员射击一次时“射中9环以上”的概率（精确到0.1），

    并简述理由.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】解决问题时需要思考：是否解决过与其类似的问题.小明从问题1解题思路中获得启发从而解决了问题2.

    问题1：如图①，在正方形ABCD中，E、F是BC、CD上两点，∠EAF＝45°.

    求证：∠AEF＝∠AEB.

    小明给出的思路为：延长EB到H，满足BH＝DF，连接AH.请完善小明的证明过程.

    问题2：如图②，在等腰直角△ABC中，∠ACB＝90°，AC＝BC＝4，D为AB中点，E、F是AC、BC边上两点，∠EDF＝45°．

    （1）求点D到EF的距离．

    （2）若AE＝a，则S△DEF＝ （用含字母a的代数式表示）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】点A、B、C、D在数轴上的位置如图1所示，已知AB=3，BC=2，CD=4．

    （1）若点C为原点，则点A表示的数是　 　；

    （2）若点A、B、C、D分别表示有理数a，b，c，d，则|a﹣c|+|d﹣b|﹣|a﹣d|=　 　；

    （3）如图2，点P、Q分别从A、D两点同时出发，点P沿线段AB以每秒1个单位长度的速度向右运动，到达B点后立即按原速折返；点Q沿线段CD以每秒2个单位长度的速度向左运动，到达C点后立即按原速折返．当P、Q中的某点回到出发点时，两点同时停止运动．

    ①当点停止运动时，求点P、Q之间的距离；

    ②设运动时间为t（单位：秒），则t为何值时，PQ=5？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】全国爱眼日是每年的6月6日，2013年世界爱眼日主题确定为“关爱青少年眼健康”，某中学为了解该校学生的视力情况，采用抽样调查的方式，从视力正常、轻度近视、中度近视、重度近视四个方面调查了若干名学生的视力情况，并根据调查结果制作了如下两幅统计图．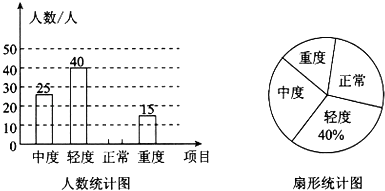

    根据图中提供的信息解答下列问题：
    （1）一共随机调查了多少人？
    （2）补全人数统计图；
    （3）若该校共有1500名学生，请你估计该校学生视力正常的人数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，矩形OABC的顶点A、C分别在x、y轴的正半轴上，点D为对角线OB的中点，点E（8，n）在边AB上，反比例函数（k≠0）在第一象限内的图象经过点D、E，且tan∠BOA=．

    （1）求反比例函数的解析式和n的值；

    （2）若反比例函数的图象与矩形的边BC交于点F，将矩形折叠，使点O与点F重合，折痕分别与x、y轴正半轴交于点H、G，求G点的坐标．

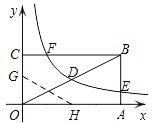
    查看答案和解析>>

    同步练习册答案