��֪����ƽ��ֱ������ϵxOy�У����κ���y=x2+bx+c��ͼ����x�ύ��A��B���㣬��A�ڵ�B����࣬�������ߵĶԳ���Ϊx=1����A������Ϊ��-1��0����
��1����������κ����Ľ���ʽ��
��2���������ߵĶ���ΪC����������һ��D������Ϊ��-3��12��������B��D��ֱ���������ߵĶԳ��ύ�ڵ�E���ʣ��Ƿ���������ĵ�F��ʹ���Ե�B��C��E��FΪ������ı�����ƽ���ı��Σ������ڣ������F�����ꣻ�������ڣ���˵�����ɣ�
��3���ڣ�2���������£�����BD�ϴ���һ��P��ʹ��ֱ��AP���ı���ACBD�ֳ��������ȵ������֣����������ʱ��P�����꣮
��������1�����ݶԳ������B�����꣬��A��B���������õ������飬���������Ľ⼴�ɣ�
��2�����ֱ��BD�����E�����꣬����ƽ���ı��ε����ʼ������F�����ꣻ
��3������ı���ACBD��������������ABP��������������P�����꣮
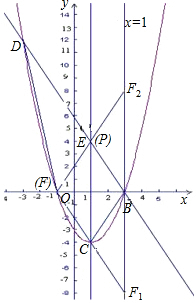
���
�⣺��1����ͼ���������ߵĶԳ���Ϊx=1����A������Ϊ��-1��0����
��B��3��0����
��
��
��ã�
��
�������ߵĽ���ʽΪy=x
2-2x-3��
��������κ����Ľ���ʽ��y=x
2-2x-3��
��2������C��������1��-4����
��D��������-3��12����
��ֱ��BD�Ľ���ʽΪy=kx+b
1��
��
��
��ã�
��
��ֱ��BD�Ľ���ʽΪy=-2k+6��
���E��������1��4����
�����⣬��B��C��E��FΪ������ı�����ƽ���ı��Σ�
���F��������3��8������3��-8����-1��0����
�𣺴��������ĵ�F��ʹ���Ե�B��C��E��FΪ������ı�����ƽ���ı��Σ���F�������ǣ�3��8������3��-8������-1��0����
��3���ı���ACBD�����=S
��ABC+S
��ABD=
��4��12+
��4��4=32��
��
S
�ı���ACBD=16��
��S
��ABC=8��
��S
��ABP=8��
���P��������Ϊ4��
��ֱ��BD�Ľ���ʽΪy=-2x+6��
���P��������1��4����
�𣺵�P�������ǣ�1��4����
������������Ҫ����������ε�������ô���ϵ��������κ��������Ԫһ�η����飬һ�κ����Ľ���ʽ��֪ʶ�����������գ����������������ʽ��м����ǽ����Ĺؼ���

 �⣺��1����ͼ���������ߵĶԳ���Ϊx=1����A������Ϊ��-1��0����
�⣺��1����ͼ���������ߵĶԳ���Ϊx=1����A������Ϊ��-1��0����

 Сѧѧϰ�ð���ϵ�д�
Сѧѧϰ�ð���ϵ�д� Сѧͬ�����������ܾ�ϵ�д�
Сѧͬ�����������ܾ�ϵ�д�

 ��ͼ����ƽ��ֱ�������У���ֱ֪��y=kx+b��ֱ��y=
��ͼ����ƽ��ֱ�������У���ֱ֪��y=kx+b��ֱ��y= ��ͼ����ƽ��ֱ������xOy�У���֪��A��-5��0����P�Ƿ���������y=
��ͼ����ƽ��ֱ������xOy�У���֪��A��-5��0����P�Ƿ���������y=