
【题目】如图,在直角坐标系中,OA=3,OC=4![]() ,点B是y轴上一动点,以AC为对角线作平行四边形ABCD.
,点B是y轴上一动点,以AC为对角线作平行四边形ABCD.
(1)求直线AC的函数解析式;
(2)设点![]() ,记平行四边形ABCD的面积为
,记平行四边形ABCD的面积为![]() ,请写出
,请写出![]() 与
与![]() 的函数关系式,并求当BD取得最小值时,函数
的函数关系式,并求当BD取得最小值时,函数![]() 的值;
的值;
(3)当点B在y轴上运动,能否使得平行四边形ABCD是菱形?若能,求出点B的坐标;若不能,说明理由.

【答案】(1)![]() ;(2) ① 当m≤4时,S=-3m+12,② 当m>4时,S=3m-12(3) (0,
;(2) ① 当m≤4时,S=-3m+12,② 当m>4时,S=3m-12(3) (0, ![]() )
)
【解析】
试题分析:(1)根据OA、OC的长度求出A、C坐标,再利用待定系数法求解即可;
(2)根据点B的坐标可得出BC的长,结合平行四边形的面积公式求出S与m的关系式,再根据AD∥y轴即可求出当BD最短时m的值,将其代入解析式即可;
(3)根据菱形的性质找出m的值,从而根据勾股定理求解即可.
试题解析:(1)直线AC的解析式为:![]()
![]()
(2) ① 当m≤4时,S=-3m+12
② 当m>4时,S=3m-12
当BD^y轴时,BD最短为4,这时B为CO的中点,
∴m=2,S=-3×2+12=6
(3)存在
当AB=CB时,平行四边形ABCD为菱形.
∴ m2+32=(4-m)2.
解得m= ![]()
![]() .
.
∴B(0,![]()
![]() ).
).


科目:初中数学 来源: 题型:
【题目】每逢金秋送爽之时,正是大闸蟹上市的旺季,也是吃蟹的最好时机,可谓膏肥黄美.


某经销商购进一批雌蟹、雄蟹共1000只,进价均为每只40元,然后以雌蟹每只75元、雄蟹每只60元的价格售完,共获利29000元.
(1)求该经销商分别购进雌蟹、雄蟹各多少只?
(2)民间有“九雌十雄”的说法,即九月吃雌蟹,十月吃雄蟹.十月份,在进价不变的情况下该经销商决定调整价格,将雌蟹的价格在九月份的基础上下调![]() (降价后售价不低于进价),雄蟹的价格上涨
(降价后售价不低于进价),雄蟹的价格上涨![]() ,同时雌蟹的销量较九月下降了
,同时雌蟹的销量较九月下降了![]() ,雄蟹的销量上升了
,雄蟹的销量上升了![]() ,结果十月份的销售额比九月份增加了1000元,求a的值.
,结果十月份的销售额比九月份增加了1000元,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以直线AB上一点O为端点作射线OC,使∠AOC=65°,将一个直角三角形的直角顶点放在点O处.(注:∠DOE=90°)
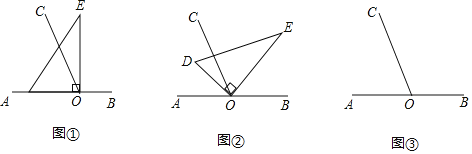
(1)如图①,若直角三角板DOE的一边OD放在射线OA上,则∠COE °.
(2)如图②,将直角三角板DOE绕点O顺时针方向转动到某个位置,若OC恰好平分∠AOE,则∠COD= °.
(3)如图③,将直角三角板DOE绕点O顺时针方向转动到某个位置,0°<∠AOD<180°,如果∠COD=![]() ∠AOE,求∠COD的度数.
∠AOE,求∠COD的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 光在反射时,光束的路径可用图(1)来表示,
光在反射时,光束的路径可用图(1)来表示,![]() 叫做入射光线,
叫做入射光线,![]() 叫做反射光线,从入射点
叫做反射光线,从入射点![]() 引出的一条垂直于镜面
引出的一条垂直于镜面![]() 的射线
的射线![]() 叫做法线,
叫做法线,![]() 与
与![]() 的夹角
的夹角![]() 叫入射角,
叫入射角,![]() 与
与![]() 的夹角
的夹角![]() 叫反射角.根据科学实验可得:
叫反射角.根据科学实验可得:![]() .则图(1)中
.则图(1)中![]() 与
与![]() 的数量关系是:____________理由:___________;
的数量关系是:____________理由:___________;

![]() 生活中我们可以运用“激光”和两块相交的平面镜进行测距.如图(2)当一束“激光”
生活中我们可以运用“激光”和两块相交的平面镜进行测距.如图(2)当一束“激光”![]() 射入到平面镜
射入到平面镜![]() 上、被
上、被![]() 反射到平面镜
反射到平面镜![]() 上,又被平面镜
上,又被平面镜![]() 反射后得到反射光线
反射后得到反射光线![]() .
.

(1)若反射光线![]() 沿着入射光线
沿着入射光线![]() 的方向反射回去,即
的方向反射回去,即![]() ,且
,且![]() ,则
,则![]() ______
______![]() ,
,![]() ______
______![]() ;
;
(2)猜想:当![]() ______
______![]() 时,任何射到平面镜
时,任何射到平面镜![]() 上的光线
上的光线![]() 经过平面镜
经过平面镜![]() 和
和![]() 的两次反射后,入射光线
的两次反射后,入射光线![]() 与反射光线
与反射光线![]() 总是平行的.请你根据所学过的知识及新知说明.
总是平行的.请你根据所学过的知识及新知说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学生小明、小华为了解本校八年级学生每周上网的时间,各自进行了抽样调查.小明调查了八年级信息技术兴趣小组中40名学生每周上网的时间,算得这些学生平均每周上网时间为2.5h;小华从全体320名八年级学生名单中随机抽取了40名学生,调查了他们每周上网的时间,算得这些学生平均每周上网时间为1.2h.小明与小华整理各自样本数据,如表所示.
时间段(h/周) | 小明抽样人数 | 小华抽样人数 |
0~1 | 6 | 22 |
1~2 | 10 | 10 |
2~3 | 16 | 6 |
3~4 | 8 | 2 |
(每组可含最低值,不含最高值)
请根据上述信息,回答下列问题:
(1)你认为哪位学生抽取的样本具有代表性?_____.
估计该校全体八年级学生平均每周上网时间为_____h;
(2)在具有代表性的样本中,中位数所在的时间段是_____h/周;
(3)专家建议每周上网2h以上(含2h)的同学应适当减少上网的时间,根据具有代表性的样本估计,该校全体八年级学生中有多少名学生应适当减少上网的时间?
查看答案和解析>>
科目:初中数学 来源: 题型:
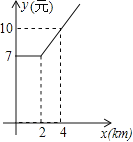
【题目】某地出租车计费方法如图,x(km)表示行驶里程,y(元)表示车费,请根据图象解答下列问题:
(1)该地出租车的起步价是 元;
(2)当x>2时,求y与x之间的函数关系式;
(3)若某乘客有一次乘出租车的里程为18km,则这位乘客需付出租车车费多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
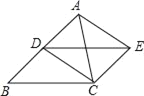
【题目】 已知,如图,点D是△ABC的边AB的中点,四边形BCED是平行四边形.
(1)求证:四边形ADCE是平行四边形;
(2)在△ABC中,若AC=BC,则四边形ADCE是 ;(只写结论,不需证明)
(3)在(2)的条件下,当AC⊥BC时,求证:四边形ADCE是正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙、丙三个教师承担本学期期末考试的第17题的网上阅卷任务,若由这三人中的某一人独立完成阅卷任务,则甲需要15小时,乙需要10小时,丙需要8小时。
(1)如果甲、乙、丙三人同时改卷,那么需要多少时间完成?
(2)如果按照甲、乙、丙、甲、乙、丙、……的次序轮流阅卷,每一轮中每人各阅卷1小时。那么要多少小时完成?
(3)能否把(2)题所说的甲、乙、丙的次序作适当调整,其余的不变,使得完成这项任务的时间至少提前半小时?(答题要求:如认为不能,需要说明理由;如认为能,请至少说出一种轮流的次序,并求出相应能提前多少时间完成阅卷任务)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2017贵州省遵义市)如图,抛物线![]() (a<0,a、b为常数)与x轴交于A、C两点,与y轴交于B点,直线AB的函数关系式为
(a<0,a、b为常数)与x轴交于A、C两点,与y轴交于B点,直线AB的函数关系式为![]() .
.
(1)求该抛物线的函数关系式与C点坐标;
(2)已知点M(m,0)是线段OA上的一个动点,过点M作x轴的垂线l分别与直线AB和抛物线交于D、E两点,当m为何值时,△BDE恰好是以DE为底边的等腰三角形?
(3)在(2)问条件下,当△BDE恰好是以DE为底边的等腰三角形时,动点M相应位置记为点M′,将OM′绕原点O顺时针旋转得到ON(旋转角在0°到90°之间);
①探究:线段OB上是否存在定点P(P不与O、B重合),无论ON如何旋转,![]() 始终保持不变,若存在,试求出P点坐标;若不存在,请说明理由;
始终保持不变,若存在,试求出P点坐标;若不存在,请说明理由;
②试求出此旋转过程中,(NA+![]() NB)的最小值.
NB)的最小值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com