
ЁОЬтФПЁПШчЭМЃЌвджБЯпABЩЯвЛЕуOЮЊЖЫЕузїЩфЯпOCЃЌЪЙЁЯAOCЃН65ЁуЃЌНЋвЛИіжБНЧШ§НЧаЮЕФжБНЧЖЅЕуЗХдкЕуOДІЃЎЃЈзЂЃКЁЯDOEЃН90ЁуЃЉ
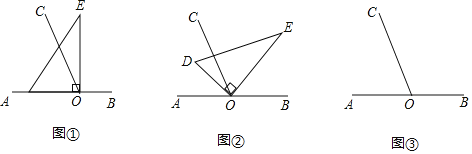
ЃЈ1ЃЉШчЭМЂйЃЌШєжБНЧШ§НЧАхDOEЕФвЛБпODЗХдкЩфЯпOAЩЯЃЌдђЁЯCOEЁЁ ЁЁЁуЃЎ
ЃЈ2ЃЉШчЭМЂкЃЌНЋжБНЧШ§НЧАхDOEШЦЕуOЫГЪБеыЗНЯђзЊЖЏЕНФГИіЮЛжУЃЌШєOCЧЁКУЦНЗжЁЯAOEЃЌдђЁЯCODЃНЁЁ ЁЁЁуЃЎ
ЃЈ3ЃЉШчЭМЂлЃЌНЋжБНЧШ§НЧАхDOEШЦЕуOЫГЪБеыЗНЯђзЊЖЏЕНФГИіЮЛжУЃЌ0ЁуЃМЁЯAODЃМ180ЁуЃЌШчЙћЁЯCODЃН![]() ЁЯAOEЃЌЧѓЁЯCODЕФЖШЪ§ЃЎ
ЁЯAOEЃЌЧѓЁЯCODЕФЖШЪ§ЃЎ
ЁОД№АИЁПЃЈ1ЃЉ25ЃЛЃЈ2ЃЉ25ЃЛЃЈ3ЃЉ51Ёу
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнЛЅгрПЩЧѓГіД№АИЃЌ
ЃЈ2ЃЉгЩНЧЦНЗжЯпЕУЁЯCOEЃНЁЯAOCЃН65ЁуЃЌдйгЩЁЯCODЃНЁЯDOEЉЁЯCOEЧѓГіД№АИЃЛ
ЃЈ3ЃЉЩшЮДжЊЪ§ЃЌНЈСЂЗНГЬЧѓНтМДПЩЃЎ
НтЃКЃЈ1ЃЉЁЯCOEЃНЁЯDOEЉЁЯAOCЃН90ЁуЉ65ЁуЃН25ЁуЃЌ
ЙЪД№АИЮЊЃК25ЃЎ
ЃЈ2ЃЉЁпOCЧЁКУЦНЗжЁЯAOEЃЌ
ЁрЁЯCOEЃНЁЯAOCЃН65ЁуЃЌ
ЁрЁЯCODЃНЁЯDOEЉЁЯCOEЃН90ЁуЉ65ЁуЃН25ЁуЃЌ
ЙЪД№АИЮЊЃК25ЃЎ
ЃЈ3ЃЉЩшЁЯCODЃНxЃЌгЩЬтвтЕУЃК
ЁЯCODЃН![]() ЁЯAOEЃЌМДЃКxЃН
ЁЯAOEЃЌМДЃКxЃН![]() ЃЈ65Ёу+x+90ЁуЃЉЃЌ
ЃЈ65Ёу+x+90ЁуЃЉЃЌ
НтЕУЃКxЃН51ЁуЃЌМДЃКЁЯCODЃН51Ёу



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЕиЮЊСЫНтЧрЩйФъЪЕСІЧщПіЃЌЯжЫцЛњГщВщСЫШєИЩУћГѕжабЇЩњНјааЪгСІЧщПіЭГМЦЃЌЗжЮЊЪгСІе§ГЃЁЂЧсЖШНќЪгЁЂжиЖШНќЪгШ§жжЧщПіЃЌВЂЛцГЩШчЭМЫљЪОЕФЬѕаЮЭГМЦЭМКЭЩШаЮЭГМЦЭМЃЈВЛЭъећЃЉЃЌЧыФуИљОнЭМжааХЯЂНтД№ЯТСаЮЪЬтЃК
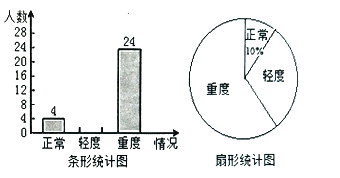
ЃЈ1ЃЉЧѓетДЮБЛГщВщЕФбЇЩњвЛЙВгаЖрЩйШЫЃП
ЃЈ2ЃЉЧѓБЛГщВщЕФбЇЩњжаЧсЖШНќЪгЕФбЇЩњШЫЪ§ЃЌВЂНЋЬѕаЮЭГМЦЭМВЙГфЭъећЃЛ
ЃЈ3ЃЉШєФГЕига![]() ЭђУћГѕжаЩњЃЌЧыЙРМЦЪгСІВЛе§ГЃЃЈАќРЈЧсЖШНќЪгЁЂжиЖШНќЪгЃЉЕФбЇЩњЙВгаЖрЩйШЫЃП
ЭђУћГѕжаЩњЃЌЧыЙРМЦЪгСІВЛе§ГЃЃЈАќРЈЧсЖШНќЪгЁЂжиЖШНќЪгЃЉЕФбЇЩњЙВгаЖрЩйШЫЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
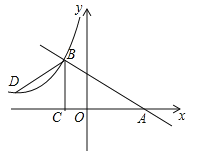
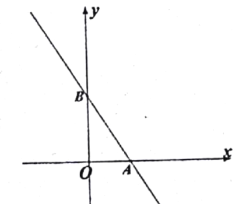
ЁОЬтФПЁПШчЭМЃЌвбжЊвЛДЮКЏЪ§y=kx+bЕФЭМЯѓгыxжсНЛгкЕуAЃЌгыЗДБШР§КЏЪ§![]() ЃЈxЃМ0ЃЉЕФЭМЯѓНЛгкЕуBЃЈЉ2ЃЌnЃЉЃЌЙ§ЕуBзїBCЁЭxжсгкЕуCЃЌЕуDЃЈ3Љ3nЃЌ1ЃЉЪЧИУЗДБШР§КЏЪ§ЭМЯѓЩЯвЛЕуЃЎ
ЃЈxЃМ0ЃЉЕФЭМЯѓНЛгкЕуBЃЈЉ2ЃЌnЃЉЃЌЙ§ЕуBзїBCЁЭxжсгкЕуCЃЌЕуDЃЈ3Љ3nЃЌ1ЃЉЪЧИУЗДБШР§КЏЪ§ЭМЯѓЩЯвЛЕуЃЎ
ЃЈ1ЃЉЧѓmЕФжЕЃЛ
ЃЈ2ЃЉШєЁЯDBC=ЁЯABCЃЌЧѓвЛДЮКЏЪ§y=kx+bЕФБэДяЪНЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкжБНЧзјБъЯЕжаЃЌвбжЊжБЯп![]() гы
гы![]() жсЯрНЛгкЕу
жсЯрНЛгкЕу![]() ЃЌгы
ЃЌгы![]() жсНЛгкЕу
жсНЛгкЕу![]() .
.
ЃЈ1ЃЉЧѓ![]() ЕФжЕМА
ЕФжЕМА![]() ЕФУцЛ§ЃЛ
ЕФУцЛ§ЃЛ
ЃЈ2ЃЉЕу![]() дк
дк![]() жсЩЯЃЌШє
жсЩЯЃЌШє![]() ЪЧвд
ЪЧвд![]() ЮЊбќЕФЕШбќШ§НЧаЮЃЌжБНгаДГіЕу
ЮЊбќЕФЕШбќШ§НЧаЮЃЌжБНгаДГіЕу![]() ЕФзјБъЃЛ
ЕФзјБъЃЛ
ЃЈ3ЃЉЕу![]() дк
дк![]() жсЩЯЃЌШєЕу
жсЩЯЃЌШєЕу![]() ЪЧжБЯп
ЪЧжБЯп![]() ЩЯЕФвЛИіЖЏЕуЃЌЕБ
ЩЯЕФвЛИіЖЏЕуЃЌЕБ![]() ЕФУцЛ§гы
ЕФУцЛ§гы![]() ЕФУцЛ§ЯрЕШЪБЃЌЧѓЕу
ЕФУцЛ§ЯрЕШЪБЃЌЧѓЕу![]() ЕФзјБъ.
ЕФзјБъ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮвУЧгУ[a]БэЪОВЛДѓгкaЕФзюДѓећЪ§,Р§Шч:[2.5]ЃН2,[3]ЃН3,[Ѓ2.5]ЃНЃ3;гУЃМaЃОБэЪОДѓгкaЕФзюаЁећЪ§,Р§Шч:ЃМ2.5ЃО=3,ЃМ4.5ЃО=5,ЃМЃ1.5ЃО=Ѓ1.НтОіЯТСаЮЪЬт.
ЃЈ1ЃЉ[Ѓ4.5]ЃН_____;ЃМ3.5ЃО=________;
ЃЈ2ЃЉШє[x]ЃН2,дђxЕФШЁжЕЗЖЮЇЪЧ________;ШєЃМyЃО=Ѓ1ЃЌдђyЕФШЁжЕЗЖЮЇЪЧ_______.
ЃЈ3ЃЉШє![]() ЃЌдђxЮЊ_________.
ЃЌдђxЮЊ_________.
ЃЈ4ЃЉвбжЊxЁЂyТњзуЗНГЬзщ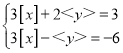
![]() ЃЌЧѓxЁЂyЕФШЁжЕЗЖЮЇ.
ЃЌЧѓxЁЂyЕФШЁжЕЗЖЮЇ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
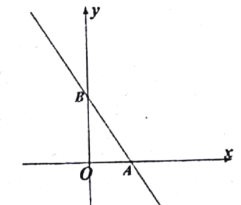
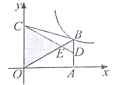
ЁОЬтФПЁПШчЭМЃЌЫФБпаЮOABCжаЃЌABЁЮOCЃЌБпOAдкxжсЕФе§АыжсЩЯЃЌOCдкyжсЕФе§АыжсЩЯЃЌЕуBдкЕквЛЯѓЯоФкЃЌЕуDЮЊABЕФжаЕуЃЌCDгыOBЯрНЛгкЕуEЃЌШєЁїBDEЁЂЁїOCEЕФУцЛ§ЗжБ№ЮЊ1КЭ9ЃЌЗДБШР§КЏЪ§y=![]() ЕФЭМЯѓОЙ§ЕуBЃЌдђk=_______.
ЕФЭМЯѓОЙ§ЕуBЃЌдђk=_______.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШЯецдФЖСЯТУцЕФВФСЯЃЌЭъГЩгаЙиЮЪЬтЃЎ
ВФСЯЃКдкбЇЯАОјЖджЕЪБЃЌРЯЪІНЬЙ§ЮвУЧОјЖджЕЕФМИКЮКЌвхЃЌвЛАуЕиЃЌЕуAЁЂBдкЪ§жсЩЯЗжБ№БэЪОгаРэЪ§aЁЂbЃЌФЧУДAЁЂBжЎМфЕФОрРыПЩБэЪОЮЊ|aЉb|ЃЎ
ЮЪЬтЃЈ1ЃЉЃКЕуAЁЂBЁЂCдкЪ§жсЩЯЗжБ№БэЪОгаРэЪ§xЁЂЉ2ЁЂ1ЃЌФЧУДAЕНBЕФОрРыгыAЕНCЕФОрРыжЎКЭПЩБэЪОЮЊЁЁЁЁ ЃЈгУКЌОјЖджЕЕФЪНзгБэЪОЃЉЃЎ
ЮЪЬтЃЈ2ЃЉЃКРћгУЪ§жсЬНОПЃКЂйевГіТњзу|xЉ3|+|x+1|=6ЕФxЕФЫљгажЕЪЧЁЁ ЁЁЁЁЁЁЃЛ
ЂкЩш|xЉ3|+|x+1|=pЃЌЕБxЕФжЕШЁдкВЛаЁгкЉ1ЧвВЛДѓгк3ЕФЗЖЮЇЪБЃЌpЕФжЕЪЧВЛБфЕФЃЌЖјЧвЪЧpЕФзюаЁжЕЃЌетИізюаЁжЕЪЧЁЁЁЁЁЁ ЃЛЕБxЕФжЕШЁдкЁЁЁЁЁЁ ЕФЗЖЮЇЪБЃЌ|x|+|xЉ2|ЕФзюаЁжЕЪЧЁЁЁЁЁЁ ЃЎ
ЮЪЬтЃЈ3ЃЉЃКЧѓ|xЉ3|+|xЉ2|+|x+1|ЕФзюаЁжЕвдМАДЫЪБxЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкжБНЧзјБъЯЕжаЃЌOA=3ЃЌOC=4![]() ЃЌЕуBЪЧyжсЩЯвЛЖЏЕуЃЌвдACЮЊЖдНЧЯпзїЦНааЫФБпаЮABCD.
ЃЌЕуBЪЧyжсЩЯвЛЖЏЕуЃЌвдACЮЊЖдНЧЯпзїЦНааЫФБпаЮABCD.
ЃЈ1ЃЉЧѓжБЯпACЕФКЏЪ§НтЮіЪНЃЛ
ЃЈ2ЃЉЩшЕу![]() ЃЌМЧЦНааЫФБпаЮABCDЕФУцЛ§ЮЊ
ЃЌМЧЦНааЫФБпаЮABCDЕФУцЛ§ЮЊ![]() ЃЌЧыаДГі
ЃЌЧыаДГі![]() гы
гы![]() ЕФКЏЪ§ЙиЯЕЪНЃЌВЂЧѓЕБBDШЁЕУзюаЁжЕЪБЃЌКЏЪ§
ЕФКЏЪ§ЙиЯЕЪНЃЌВЂЧѓЕБBDШЁЕУзюаЁжЕЪБЃЌКЏЪ§![]() ЕФжЕЃЛ
ЕФжЕЃЛ
ЃЈ3ЃЉЕБЕуBдкyжсЩЯдЫЖЏЃЌФмЗёЪЙЕУЦНааЫФБпаЮABCDЪЧСтаЮЃПШєФмЃЌЧѓГіЕуBЕФзјБъЃЛШєВЛФмЃЌЫЕУїРэгЩ.

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЯТСаВЛЕШЪНБфаЮЃЌГЩСЂЕФЪЧЃЈ ЃЉ
A.ШєmЃМnЃЌдђmЃ2ЃМnЃ2B.ШєmЃМnЃЌдђ2ЃmЃМ2Ѓn
C.ШєmЃМnЃЌдђЃ2mЃМЃ2nD.ШєmЃМnЃЌдђ![]()
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com