练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

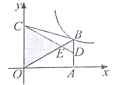
    【题目】如图，四边形OABC中，AB∥OC，边OA在x轴的正半轴上，OC在y轴的正半轴上，点B在第一象限内，点D为AB的中点，CD与OB相交于点E，若△BDE、△OCE的面积分别为1和9，反比例函数y=的图象经过点B，则k=_______.

    【答案】16

    【解析】分析：根据题意得S△BDE：S△OCE=1:9，故BD：OC=1:3，设D（a,b）则A(a,0),B(a,2b)，得C(0,3b)，由S△OCE=9得ab=8，故可得解.

    详解：设D（a,b）则A(a,0),B(a,2b)

    ∵S△BDE：S△OCE=1:9

    ∴BD：OC=1:3

    ∴C(0,3b)

    ∴S△OCE=3ba× =9

    解得ab=8

    k=a×2b=2ab=2×8=16

    故答案为：16.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】材料阅读：对于一个圆和一个正方形给出如下定义：若圆上存在到此正方形四条边距离都相等的点，则称这个圆是该正方形的“等距圆”．

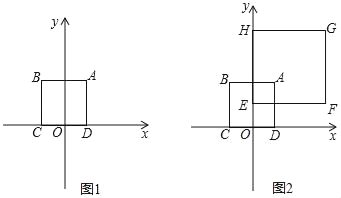
    如图1，在平面直角坐标系xOy中，正方形ABCD的顶点A的坐标为（2，4），顶点C、D在x轴上，且点C在点D的左侧．

    （1）当r=2时，在P1（2，0），P2（﹣4，2），P3（2，2），P4（2﹣2，0）中可以成为正方形ABCD的“等距圆”的圆心的是　 　；

    （2）若点P坐标为（﹣2，﹣1），则当⊙P的半径r=　 　时，⊙P是正方形ABCD的“等距圆”．试判断此时⊙P与直线BD的位置关系？并说明理由．

    （3）如图2，在正方形ABCD所在平面直角坐标系xOy中，正方形EFGH的顶点F的坐标为（8，2），顶点E、H在y轴上，且点H在点E的上方．若⊙P同时为上述两个正方形的“等距圆”，且与BC所在直线相切，求⊙P的圆心P的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，一架梯子长25米，斜靠在一面墙上，梯子底端离墙7米。

    （1）这个梯子的顶端离地面有多高？

    （2）如果梯子的顶端下滑了4米，那么梯子的底端在水平方向滑动了几米？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知点（﹣1，y1），（2，y2），在反比例函数y＝﹣的图象上，则下列关系式正确的是（　　）

    A.y3＜y2＜y1B.y2＜y3＜y1

    C.y3＜y1＜y2D.y2＜y1＜y3

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，以直线AB上一点O为端点作射线OC，使∠AOC＝65°，将一个直角三角形的直角顶点放在点O处．（注：∠DOE＝90°）

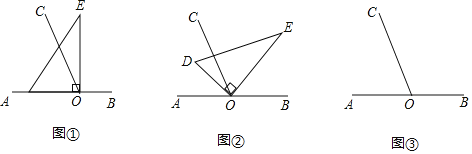
    （1）如图①，若直角三角板DOE的一边OD放在射线OA上，则∠COE　 　°．

    （2）如图②，将直角三角板DOE绕点O顺时针方向转动到某个位置，若OC恰好平分∠AOE，则∠COD＝　 　°．

    （3）如图③，将直角三角板DOE绕点O顺时针方向转动到某个位置，0°＜∠AOD＜180°，如果∠COD＝∠AOE，求∠COD的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】为了解社区居民最喜欢的支付方式，某兴趣小组对龙湖社区内20~60岁年龄段的部分居民展开了随机问卷调查（每人只能选择其中一项），并将调查数据整理后绘成如下两幅不完整的统计图.请根据图中信息解答下列问题：

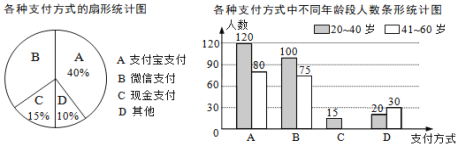
    （1）求参与问卷调查的总人数.

    （2）补全条形统计图.

    （3）该社区中20~60岁的居民约4000人，估算这些人中最喜欢微信支付方式的人数.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】光在反射时，光束的路径可用图（1）来表示，叫做入射光线，叫做反射光线，从入射点引出的一条垂直于镜面的射线叫做法线，与的夹角叫入射角，与的夹角叫反射角.根据科学实验可得：.则图（1）中与的数量关系是：____________理由：___________；

    生活中我们可以运用“激光”和两块相交的平面镜进行测距.如图（2）当一束“激光”射入到平面镜上、被反射到平面镜上，又被平面镜反射后得到反射光线.

    （1）若反射光线沿着入射光线的方向反射回去，即，且，则______，______；

    （2）猜想：当______时，任何射到平面镜上的光线经过平面镜和的两次反射后，入射光线与反射光线总是平行的.请你根据所学过的知识及新知说明.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

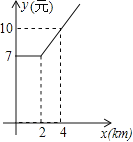
    【题目】某地出租车计费方法如图，x（km）表示行驶里程，y（元）表示车费，请根据图象解答下列问题：

    （1）该地出租车的起步价是 元；

    （2）当x＞2时，求y与x之间的函数关系式；

    （3）若某乘客有一次乘出租车的里程为18km，则这位乘客需付出租车车费多少元？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】)图①中是一座钢管混凝土系杆拱桥，桥的拱肋ACB可视为抛物线的一部分(如图②)，桥面(视为水平的)与拱肋用垂直于桥面的系杆连接，测得拱肋

    的跨度AB为200米，与AB中点O相距20米处有一高度为48米的系杆．

    【1】求正中间系杆OC的长度；

    【2】若相邻系杆之间的间距均为5米(不考虑系杆的粗细)，则是否存在一根系杆的长度恰好是OC长度的一半？请说明理由．

    查看答案和解析>>

    同步练习册答案