
【题目】如图,在边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上,请按要求完成下列各题: 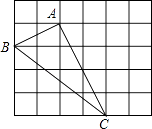
(1)画线段AD∥BC且使AD=BC,连接CD;
(2)线段AC的长为 , CD的长为 , AD的长为;
(3)△ACD为三角形,四边形ABCD的面积为 .
【答案】
(1)解:如图所示:
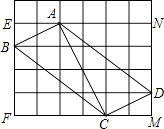
(2)2 ![]() ;
;![]() ;5
;5
(3)直角;10
【解析】解:(1)如图所示:(2)AC= ![]() =2
=2 ![]() ; CD=
; CD= ![]() =
= ![]() ;
;
AD= ![]() =5;(3)∵(2
=5;(3)∵(2 ![]() )2+(
)2+( ![]() )2=52 ,
)2=52 ,
∴△ACD是直角三角形,
S四边形ABCD=4×6﹣ ![]() ×2×1﹣
×2×1﹣ ![]() ×4×3﹣
×4×3﹣ ![]() ×2×1﹣
×2×1﹣ ![]() ×3×4=10.
×3×4=10.
所以答案是:2 ![]() ,
, ![]() ,5;直角,10.
,5;直角,10.
【考点精析】解答此题的关键在于理解勾股定理的概念的相关知识,掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2,以及对勾股定理的逆定理的理解,了解如果三角形的三边长a、b、c有下面关系:a2+b2=c2,那么这个三角形是直角三角形.


科目:初中数学 来源: 题型:
【题目】由于空气污染,气候干旱等因素,今年流感大肆流行,根据山东省卫计委统计,截止2018年1月,本年度全省共报告流感样病例442000例,其中0﹣14岁年龄组占到总病例数的88.09%,用科学记数法表示数字442000是( )
A. 4.42×103 B. 442×103 C. 4.42×105 D. 442×105
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,用同样规格的黑白两色正方形瓷砖铺设矩形地面,请观察下列图形,探究并观察下列问题。
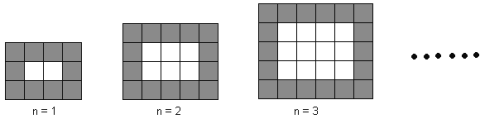
(1)在第4个图中,共有白色瓷砖 块;在第![]() 个图中,共有白色瓷砖 块;
个图中,共有白色瓷砖 块;
(2)在第4个图中,共有瓷砖 块;在第![]() 个图中,共有瓷砖 块;
个图中,共有瓷砖 块;
(3)如果每块黑瓷砖4元,白瓷砖3元,铺设当![]() 时,共需花多少钱购买瓷砖?
时,共需花多少钱购买瓷砖?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知代数式![]() ,当
,当![]() 时,该代数式的值为-1.
时,该代数式的值为-1.
(1)求![]() 的值。
的值。
(2)已知当![]() 时,该代数式的值为-1,求
时,该代数式的值为-1,求![]() 的值。
的值。
(3)已知当![]() 时,该代数式的值为9,试求当
时,该代数式的值为9,试求当![]() 时该代数式的值。
时该代数式的值。
(4)在第(3)小题已知条件下,若有![]() 成立,试比较
成立,试比较![]() 与
与![]() 的大小。
的大小。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AB=BC,对角线BD平分∠ABC,P是BD上一点,过点P作PM⊥AD,PN⊥CD,垂足分别为M,N. 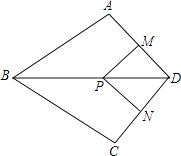
(1)求证:∠ADB=∠CDB;
(2)若∠ADC=90°,求证:四边形MPND是正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,现有一张边长为4的正方形纸片ABCD,点P为正方形AD边上的一点(不与点A、点D重合)将正方形纸片折叠,使点B落在P处,点C落在G处,PG交DC于H,折痕为EF,连接BP、BH. 
(1)求证:∠APB=∠BPH;
(2)当点P在边AD上移动时,△PDH的周长是否发生变化?并证明你的结论;
(3)设AP为x,四边形EFGP的面积为S,求出S与x的函数关系式,试问S是否存在最小值?若存在,求出这个最小值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A、B两厂在公路的同侧,现欲在公路边建一货场C.
(1)若要使货场到两厂的距离相等,请在图1中作出此时货场的位置.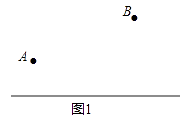
(2)若要求所修公路(即A、B两厂到货场的距离之和)最短,请在图2中作出货场的位置.(用尺规作图,保留作图痕迹,不必写作法)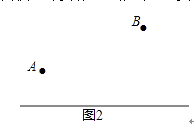
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com