
【题目】如图,用同样规格的黑白两色正方形瓷砖铺设矩形地面,请观察下列图形,探究并观察下列问题。
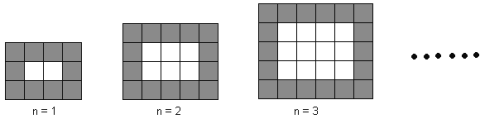
(1)在第4个图中,共有白色瓷砖 块;在第![]() 个图中,共有白色瓷砖 块;
个图中,共有白色瓷砖 块;
(2)在第4个图中,共有瓷砖 块;在第![]() 个图中,共有瓷砖 块;
个图中,共有瓷砖 块;
(3)如果每块黑瓷砖4元,白瓷砖3元,铺设当![]() 时,共需花多少钱购买瓷砖?
时,共需花多少钱购买瓷砖?
【答案】(1)20,n2+n;(2)42,(n+2)(n+3);(3)514元
【解析】
试题分析:(1)通过观察发现规律,然后将n=4代入即可;
(2)将黑色瓷砖和白色瓷砖加在一起即可得到答案;
(3)求出当n=10时黑色和白色瓷砖的个数,然后计算总费用即可.
(1)通过观察图形可知,当n=1时,用白瓷砖2块,黑瓷砖10块;
当n=2时,用白瓷砖6块,黑瓷砖14块;
当n=3时,用白瓷砖12块,黑瓷砖18块;
可以发现,需要白瓷砖的数量和图形数之间存在这样的关系,即白瓷砖块数等于图形数的平方加上图形数;
需要黑瓷砖的数量和图形数之间存在这样的关系,即黑瓷砖块数等于图形数的4倍加上图形数.
所以,在第n个图形中,白瓷砖的块数可用含n的代数式表示为![]() ;
;
黑瓷砖的块数可用含n的代数式表示为4n+6.
∴当n=4时,白色瓷砖有![]() 块;
块;
(2)由(1)可得总块数可表示为![]() ;
;
(3)观察图形可知,每-横行有白砖(n+1)块,每-竖列有白砖n块,
因而白砖总数是n(n+1)块,n=10时,白砖为10×11=110(块),黑砖数为46(块).
故总钱数为110×3+46×4=330+184=514(元),
答:共花514元钱购买瓷砖.


科目:初中数学 来源: 题型:
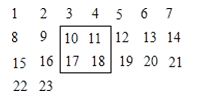
【题目】把2100个连续的正整数1、2、3、……、2100,按如图方式排列成一个数表,如图用一个正方形框在表中任意框住4个数,设左上角的数为x.
(1) 另外三个数用含x的式子表示出来,从小到大排列是___________
(2) 被框住4个数的和为416时,x值为多少?
(3) 能否框住四个数和为324?若能,求出x值;若不能,说明理由
(4) 从左到右,第1至第7列各数之和分别为a1、a2、a3、a4、a5、a6、a7,请直接写出7个数中最大的数与最小的数之差.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一组数据:60,30,40,50,70,这组数据的平均数和中位数分别是( )
A. 60,50 B. 50,60 C. 50,50 D. 60,60
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图, ![]() 是线段
是线段![]() 上一点,
上一点, ![]() ,
, ![]() .
.
![]()
(![]() )
)![]() __________
__________ ![]() ;
;
(![]() )动点
)动点![]() 、
、![]() 分别从
分别从![]() 、
、![]() 同时出发,点
同时出发,点![]() 以
以![]() 的速度沿
的速度沿![]() 向右运动,终点为
向右运动,终点为![]() ;点
;点![]() 以
以![]() 的速度沿
的速度沿![]() 向左运动,终点为
向左运动,终点为![]() .当一个点到达终点,另一个点也随之停止运动.求运动多少秒时,
.当一个点到达终点,另一个点也随之停止运动.求运动多少秒时, ![]() 、
、![]() 、
、![]() 三点,有一点恰好是以另两点为端点的线段的中点?
三点,有一点恰好是以另两点为端点的线段的中点?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上,请按要求完成下列各题: 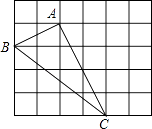
(1)画线段AD∥BC且使AD=BC,连接CD;
(2)线段AC的长为 , CD的长为 , AD的长为;
(3)△ACD为三角形,四边形ABCD的面积为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知某开发区有一块四边形的空地ABCD,如图所示,经测量∠A=90°,AB=3m,BC=12m,CD=13m,DA=4m,求这块空地的面积? 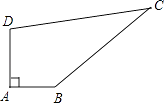
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com