
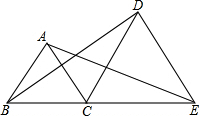
 点B、C、E在同一直线上,△ABC和△DCE均为等边三角形,连结AE,DB,求证:AE=DB.
点B、C、E在同一直线上,△ABC和△DCE均为等边三角形,连结AE,DB,求证:AE=DB. 分析 根据等边三角形边长相等的性质得出BC=AC,CD=CE,∠BCA=∠DCE=60°,求出∠BCD=∠ACE,根据SAS推出△BCD≌△ACE,根据全等三角形对应边相等的性质即可求得AE=BD.
解答 证明:∵△ABC、△DCE均为等边三角形,
∴BC=AC,CD=CE,∠BCA=∠DCE=60°,
∴∠BCA+∠ACD=∠DCE+∠ACD,
即∠BCD=∠ACE,
∵在△ACE和△BCD中,
$\left\{\begin{array}{l}{AC=BC}\\{∠ACE=∠BCD}\\{CE=CD}\end{array}\right.$
∴△ACE≌△BCD(SAS),
∴AE=BD.
点评 本题考查了等边三角形的性质、全等三角形的判定与性质的应用,能求出△ACE≌△BCD是解此题的关键.


科目:初中数学 来源: 题型:解答题
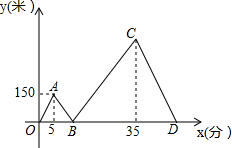 甲、乙两人从学校出发沿同一路线步行到距学校1500米处的图书馆看书,甲与乙在行进过程中以各自的速度匀速行走,甲比乙先出发5分钟,乙比甲先到达图书馆,甲、乙两人间的距离y(米)与甲的行走时间x(分)之间的函数图象如图所示.
甲、乙两人从学校出发沿同一路线步行到距学校1500米处的图书馆看书,甲与乙在行进过程中以各自的速度匀速行走,甲比乙先出发5分钟,乙比甲先到达图书馆,甲、乙两人间的距离y(米)与甲的行走时间x(分)之间的函数图象如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,△ABC面积为1,第一次操作:分别延长AB,BC,CA至点A1,B1,C1,使A1B=AB,B1C=BC,C1A=CA,顺次连接A1,B1,C1,得到△A1B1C1.第二次操作:分别延长A1B1,B1C1,C1A1至点A2,B2,C2,使A2B1=A1B1,B2C1=B1C1,C2A1=C1A1,顺次连接A2,B2,C2,得到△A2B2C2,…按此规律,要使得到的三角形的面积超过2016,最少经过( )次操作.
如图,△ABC面积为1,第一次操作:分别延长AB,BC,CA至点A1,B1,C1,使A1B=AB,B1C=BC,C1A=CA,顺次连接A1,B1,C1,得到△A1B1C1.第二次操作:分别延长A1B1,B1C1,C1A1至点A2,B2,C2,使A2B1=A1B1,B2C1=B1C1,C2A1=C1A1,顺次连接A2,B2,C2,得到△A2B2C2,…按此规律,要使得到的三角形的面积超过2016,最少经过( )次操作.| A. | 6 | B. | 5 | C. | 4 | D. | 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,平面直角坐标系中,△ABC的顶点坐标分别是A(-3,1),B(-1,1),C(-2,2),当直线y﹦-$\frac{1}{2}$x+b与△ABC有公共点时,b的取值范围是( )
如图,平面直角坐标系中,△ABC的顶点坐标分别是A(-3,1),B(-1,1),C(-2,2),当直线y﹦-$\frac{1}{2}$x+b与△ABC有公共点时,b的取值范围是( )| A. | -1≤b≤$\frac{1}{2}$ | B. | -1≤b≤1 | C. | -$\frac{1}{2}$≤b≤1 | D. | -$\frac{1}{2}$≤b≤$\frac{1}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
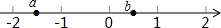 我们可以计算出
我们可以计算出查看答案和解析>>
科目:初中数学 来源: 题型:填空题
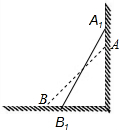 如图所示,一架5米长的消防梯子斜靠在一竖直的墙AC上,梯足(点B)离墙底端(C点)的距离为3米,如果梯足内移1.6米至点B处,则梯子顶端沿墙垂直上移0.8米.
如图所示,一架5米长的消防梯子斜靠在一竖直的墙AC上,梯足(点B)离墙底端(C点)的距离为3米,如果梯足内移1.6米至点B处,则梯子顶端沿墙垂直上移0.8米.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1000(x+x)=a | B. | 1000(1-2x)=a | C. | 1000(1+x)2=a | D. | 1000(1+2x)2=a |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com