
分析 利用完全平方公式的性质,将x-x-1=-1,变形(x-x-1)2=(-1)2,得出x2+x-2的值,进而得出(x+x-1)的值,然后利用立方差公式进行变形,得出它的值.
解答 解:∵x-x-1=-1,(x-x-1)2=(-1)2,
∴x2+x-2-2=1,xx-1=1,
∴x2+x-2=3,
∵(x+x-1)2=x2+x-2+2xx-1=3+2=5,
∴x+x-1=±$\sqrt{5}$,
∵x<0,∴x+x-1=-$\sqrt{5}$,
∵x3+x-3=(x+x-1)(x2+x-2-xx-1),
=-$\sqrt{5}$×(3-1),
=-2$\sqrt{5}$,
故答案为:-2$\sqrt{5}$.
点评 此题主要考查了完全平方公式与立方和公式的应用,解决问题的关键是灵活分解因式,进行求解.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
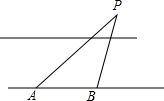 在沿东西走向的河岸南岸,某人自西向东行走,在A处测得河北岸建筑物P在北偏东60°的方向上,某人由A向东走400米到达B处时,在B处测得河北岸物P在北偏东45°的方向上,如果建筑物P距河北岸100米,求河宽.(人与河的距离忽略不计,$\sqrt{3}$≈1.7)
在沿东西走向的河岸南岸,某人自西向东行走,在A处测得河北岸建筑物P在北偏东60°的方向上,某人由A向东走400米到达B处时,在B处测得河北岸物P在北偏东45°的方向上,如果建筑物P距河北岸100米,求河宽.(人与河的距离忽略不计,$\sqrt{3}$≈1.7)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com