
(7分)如图,在正方形ABCD中,E为CD边上一点,F为BC延长线上一点,且CE=CF,BE与DF之间有怎样的关系?说明理由.

BE⊥DF,BE=DF
【解析】
试题分析:根据正方形的性质可得BC=DC,∠BCD=∠DCF=90°,然后利用“边角边”证明△BCE和△DCF全等,即可.
试题解析::∵四边形ABCD是正方形,
∴BC=DC,∠BCD=∠DCF=90°,
在△BCE和△DCF中,
∵ BC=DC,∠BCD=∠DCF=90°,CE=CF ,
∴△BCE≌△DCF(SAS),
∴BE=DF.
延长BE角DF与点H
∵△BCE≌△DCF
∴∠EBC=∠FDC,
∵∠FDC+∠F=90°,
∴∠EBC+∠F=90°,
∴∠BHF=90°,
∴BE⊥DF.

考点:1. 全等三角形的判定与性质;2.正方形的性质.
考点分析: 考点1:四边形 四边形:四边形的初中数学中考中的重点内容之一,分值一般为10-14分,题型以选择,填空,解答证明或融合在综合题目中为主,难易度为中。主要考察内容:①多边形的内角和,外角和等问题②图形的镶嵌问题③平行四边形,矩形,菱形,正方形,等腰梯形的性质和判定。突破方法:①掌握多边形,四边形的性质和判定方法。熟记各项公式。②注意利用四边形的性质进行有关四边形的证明。③注意开放性题目的解答,多种情况分析。 试题属性

科目:初中数学 来源:2014-2015学年湖北省九年级3月联考数学试卷(解析版) 题型:解答题
(本题满分8分)如图,在边长为1的正方形组成的网格中,△ABC的顶点均在格点上,点A、B、C的坐标分别是A(-2,3)、B(-1,2)、C(-3,1),△ABC绕点O顺时针旋转90°后得到△A1B1C1.
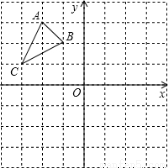
(1)在正方形网格中作出△A1B1C1;
(2)求点A经过的路径弧AA1的长度;(结果保留π)
(3)在y轴上找一点D,使DB+DB1的值最小,并直接写出D点坐标.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年湖北省九年级3月联考数学试卷(解析版) 题型:选择题
如图,把一块含有30°角(∠A=30°)的直角三角板ABC的直角顶点放在矩形桌面CDEF的一个顶点C处,桌面的另一个顶点F与三角板斜边相交于点F,如果∠1=40°,那么∠AFE( ).
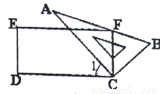
A.50° B.40° C.20° D.10°
查看答案和解析>>
科目:初中数学 来源:2014-2015学年陕西省西安市七年级下学期第一次月考数学试卷(解析版) 题型:选择题
有三个连续奇数,若中间一个是a,则它们三个数的积为( )
A、a3-4a B、a3-6a C、4a3-a D、4a3-6a
查看答案和解析>>
科目:初中数学 来源:2014-2015学年辽宁省丹东市九年级上学期第一次月考数学试卷(解析版) 题型:填空题
等腰ΔABC两边的长分别是一元二次方程x-5x+6=0的两个根,则这个等腰三角形的周长是
查看答案和解析>>
科目:初中数学 来源:2014-2015学年辽宁省丹东市九年级上学期第一次月考数学试卷(解析版) 题型:填空题
在菱形ABCD中,对角线AC与BD相交于点O,∠BAD=60,BD=6,则这个菱形的面积为 .
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省七年级上学期第一次质检数学试卷(解析版) 题型:选择题
下列各数中:+3、3、-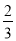 、9、
、9、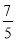 、-(-8)、0、-|+3|,负有理数有( )
、-(-8)、0、-|+3|,负有理数有( )
A.2个 B.3个 C.4个 D.5个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com