
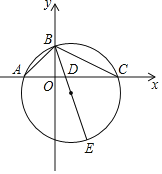
【题目】在平面直角坐标系中,点A、B、C的坐标分别为![]() 、
、![]() 、
、![]() ,点E是
,点E是![]() 的外接圆上一点,BE交线段AC于点D,若
的外接圆上一点,BE交线段AC于点D,若![]() ,则点D的坐标为______.
,则点D的坐标为______.
【答案】![]()
【解析】
连接CE,过E作EF⊥AC于F,根据已知条件得到OA=OB=2,OC=4,得到△OBA是等腰直角三角形,得到∠BAC=45°,根据圆周角定理得到∠BEC=∠BAC=45°,推出△BCE是等腰直角三角形,求得BC=CE,根据全等三角形的性质得到E(2,﹣4),待定系数法得到直线BE的解析式为y=﹣3x+2,于是得到结论.
连接CE,过E作EF⊥AC于F.
∵点A、B、C的坐标分别为(﹣2,0)、(0,2)、(4,0),∴OA=OB=2,OC=4,∴△OBA是等腰直角三角形,∴∠BAC=45°,∴∠BEC=∠BAC=45°.
∵∠DBC=45°,∴∠BCE=90°,∴△BCE是等腰直角三角形,∴BC=CE.
∵∠CBO+∠BCO=∠BOC+∠ECF=90°,∴∠OBC=∠FCE.
在△OBC与△FCE中,∵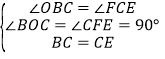 ,∴△OBC≌△FCE(AAS),∴CF=OB=2,EF=OC=4,∴OF=2,∴E(2,﹣4),设直线BE的解析式为y=kx+b,∴
,∴△OBC≌△FCE(AAS),∴CF=OB=2,EF=OC=4,∴OF=2,∴E(2,﹣4),设直线BE的解析式为y=kx+b,∴![]() ,∴
,∴![]() ,∴直线BE的解析式为y=﹣3x+2,当y=0时,x
,∴直线BE的解析式为y=﹣3x+2,当y=0时,x![]() ,∴D(
,∴D(![]() ,0).
,0).
故答案为:(![]() ,0).
,0).


 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案科目:初中数学 来源: 题型:
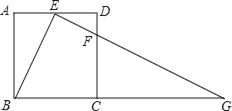
【题目】如图,在正方形ABCD中,E、F分别是边AD、CD上的点,AE=ED,DF:DC=1:4,连接EF并延长交BC的延长线于点G.
(1)求证:△ABE∽△DEF;
(2)若正方形的边长为10,求BG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:在一次数学社团活动课上,同学们测量一座古塔CD的高度,他们首先在A处安置测量器,测得塔顶C的仰角∠CFE=30°,然后往塔的方向前进100米到达B处,此时测得塔顶C的仰角∠CGE=60°,已知测量器高1.5米,请你根据以上数据计算出古塔CD的高度.(保留根号)
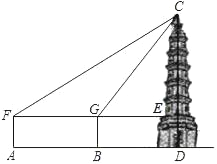
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:在Rt△ABC中,∠B=90°,BC=4cm,AB=8cm,D、E、F分别为AB、AC、BC边上的中点.若P为AB边上的一个动点,PQ∥BC,且交AC于点Q,以PQ为一边,在点A的异侧作正方形PQMN,记正方形PQMN与矩形EDBF的公共部分的面积为y.
(1)如图,当AP=3cm时,求y的值;
(2)设AP=xcm,试用含x的代数式表示y(cm2);
(3)当y=2cm2时,试确定点P的位置.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是![]()
![]()
A. 某种彩票的中奖机会是![]() 则买100张这种彩票一定会中奖
则买100张这种彩票一定会中奖
B. 为了解全国中学生的睡眠情况,应该采用普查的方式
C. 一组数据3,4,5,5,5,6,10的平均数大于中位数
D. 同时抛掷两枚均匀的硬币,出现一枚正面朝上且另一枚反面朝上的概率是![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是二次函数y=ax2+bx+c(a,b,c是常数,a≠0)图象的一部分,与x轴的交点A在点(2,0)和(3,0)之间,对称轴是x=1.对于下列说法:①ab<0;②2a+b=0;③3a+c>0;④a+b≥m(am+b)(m为实数);⑤当﹣1<x<3时,y>0,其中正确的是( )

A. ①②④ B. ①②⑤ C. ②③④ D. ③④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某种蔬菜每千克售价![]() (元)与销售月份
(元)与销售月份![]() 之间的关系如图1所示,每千克成本
之间的关系如图1所示,每千克成本![]() (元)与销售月份
(元)与销售月份![]() 之间的关系如图2所示,其中图1中的点在同一条线段上,图2中的点在同一条抛物线上,且抛物线的最低点的坐标为(6,1).
之间的关系如图2所示,其中图1中的点在同一条线段上,图2中的点在同一条抛物线上,且抛物线的最低点的坐标为(6,1).
(1)求出![]() 与
与![]() 之间满足的函数表达式,并直接写出
之间满足的函数表达式,并直接写出![]() 的取值范围;
的取值范围;
(2)求出![]() 与
与![]() 之间满足的函数表达式;
之间满足的函数表达式;
(3)设这种蔬菜每千克收益为![]() 元,试问在哪个月份出售这种蔬菜,
元,试问在哪个月份出售这种蔬菜,![]() 将取得最大值?并求出此最大值.(收益=售价-成本)
将取得最大值?并求出此最大值.(收益=售价-成本)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD是△ABC的角平分线,线段AD的垂直平分线分别交AB和AC于点E、F,连接DE、DF.
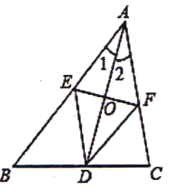
(1)试判定四边形AEDF的形状,并证明你的结论.
(2)若DE=13,EF=10,求AD的长.
(3)△ABC满足什么条件时,四边形AEDF是正方形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知点A的坐标是(4,0),并且OA=OC=4OB,动点P在过A,B,C三点的抛物线上.
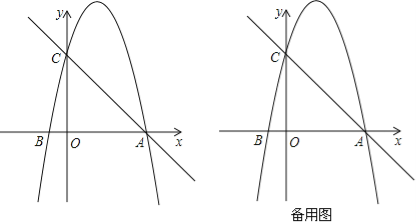
(1)求抛物线的解析式;
(2)是否存在点P,使得△ACP是以AC为直角边的直角三角形?若存在,求出所有符合条件的点P的坐标;若不存在,说明理由;
(3)过动点P作PE垂直于y轴于点E,交直线AC于点D,过点D作x轴的垂线.垂足为F,连接EF,当线段EF的长度最短时,求出点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com