
【题目】某种蔬菜每千克售价![]() (元)与销售月份
(元)与销售月份![]() 之间的关系如图1所示,每千克成本
之间的关系如图1所示,每千克成本![]() (元)与销售月份
(元)与销售月份![]() 之间的关系如图2所示,其中图1中的点在同一条线段上,图2中的点在同一条抛物线上,且抛物线的最低点的坐标为(6,1).
之间的关系如图2所示,其中图1中的点在同一条线段上,图2中的点在同一条抛物线上,且抛物线的最低点的坐标为(6,1).
(1)求出![]() 与
与![]() 之间满足的函数表达式,并直接写出
之间满足的函数表达式,并直接写出![]() 的取值范围;
的取值范围;
(2)求出![]() 与
与![]() 之间满足的函数表达式;
之间满足的函数表达式;
(3)设这种蔬菜每千克收益为![]() 元,试问在哪个月份出售这种蔬菜,
元,试问在哪个月份出售这种蔬菜,![]() 将取得最大值?并求出此最大值.(收益=售价-成本)
将取得最大值?并求出此最大值.(收益=售价-成本)

【答案】(1)y1=﹣![]() x+7(3≤x≤6);(2)y2=
x+7(3≤x≤6);(2)y2=![]() (x﹣6)2+1;(3)5月出售这种蔬菜,每千克收益最大
(x﹣6)2+1;(3)5月出售这种蔬菜,每千克收益最大
【解析】
(1)设y1=kx+b,y2=a(x-b)2+c,代入各点求出未知量,(2)收益=售价-成本,列出函数解析式,求出最大值.
(1)设y1=kx+b,
∵直线经过(3,5)、(6,3),
![]() ,解得:
,解得: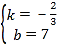 ,
,
∴y1=﹣![]() x+7(3≤x≤6),
x+7(3≤x≤6),
(2)设y2=a(x﹣6)2+1,
把(3,4)代入得:4=a(3﹣6)2+1,
解得a=![]() ,
,
∴y2=![]() (x﹣6)2+1,
(x﹣6)2+1,
(3)由题意得:w=y1﹣y2=﹣![]() x+7﹣[
x+7﹣[![]() (x﹣6)2+1],
(x﹣6)2+1],
=﹣![]() x2+
x2+![]() =﹣
=﹣![]() ,
,
当x=5时,y最大值=![]() .
.
故5月出售这种蔬菜,每千克收益最大.


科目:初中数学 来源: 题型:
【题目】下列命题的逆命题成立的是( ).
A.全等三角形的对应角相等
B.若三角形的三边满足![]() ,则该三角形是直角三角形
,则该三角形是直角三角形
C.对顶角相等
D.同位角互补,两直线平行
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,已知直线y=-2x+4与x轴、y轴分别交于点A、C,以OA、OC为边在第一象限内作长方形OABC.

(1)求点A、C的坐标;
(2)将△ABC对折,使得点A的与点C重合,折痕交AB于点D,求直线CD的解析式(图②);
(3)在坐标平面内,是否存在点P(除点B外),使得△APC与△ABC全等?若存在,请直接写出所有符合条件的点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】王老师将![]() 个黑球和若干个白球放入一个不透明的口袋并搅匀,让若干学生进行摸球实验,每次摸出一个球(有放回),下表是活动进行中的一组统计数据.
个黑球和若干个白球放入一个不透明的口袋并搅匀,让若干学生进行摸球实验,每次摸出一个球(有放回),下表是活动进行中的一组统计数据.
摸球的次数 |
|
|
|
|
|
|
摸到黑球的次数 |
|
|
|
|
|
|
摸到黑球的频率 |
|
|
|
|
|
![]() 补全上表中的有关数据,根据上表数据估计从袋中摸出一个球是黑球的概率是________(精确到0.01);
补全上表中的有关数据,根据上表数据估计从袋中摸出一个球是黑球的概率是________(精确到0.01);
![]() 估算袋中白球的个数;
估算袋中白球的个数;
![]() 在
在![]() 的条件下,若小强同学有放回地连续两次摸球,用画树状图或列表的方法计算他两次都摸出白球的概率.
的条件下,若小强同学有放回地连续两次摸球,用画树状图或列表的方法计算他两次都摸出白球的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长方形纸片ABCD中,AB=4,BC=6,点E在AB边上,将纸片沿CE折叠,点B落在点F处,EF,CF分别交AD于点G,H,且EG=GH,则AE的长为( )
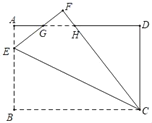
A. ![]() B. 1C.
B. 1C. ![]() D. 2
D. 2
查看答案和解析>>
科目:初中数学 来源: 题型:
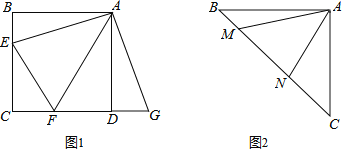
【题目】(1)如图,正方形ABCD中,点E,F分别在边BC,CD上,∠EAF=45°,延长CD到点G,使DG=BE,连结EF,AG.求证:EF=FG.
(2)如图,等腰直角三角形ABC中,∠BAC=90°,AB=AC,点M,N在边BC上,且∠MAN=45°,若BM=1,CN=3,求MN的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】[问题情境]
已知矩形的面积为一定值1,当该矩形的一组邻边分别为多少时,它的周长最小?最小值是多少?
[数学模型]
设该矩形的一边长为x,周长为L,则L与x的函数表达式为 .
[探索研究]
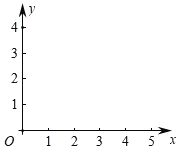
小彬借鉴以前研究函数的经验,先探索函数![]() 的图象性质.
的图象性质.
(1)结合问题情境,函数![]() 的自变量x的取值范围是 ,
的自变量x的取值范围是 ,
如表是y与x的几组对应值.
x | … |
|
|
| 1 | 2 | 3 | m | … |
y | … | 4 | 3 | 2 | 2 | 2 | 3 | 4 | … |
①直接写出m的值;
②画出该函数图象,结合图象,得出当x= 时,y有最小值,y的最小值为 .
[解决问题]
(2)直接写出“问题情境”中问题的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
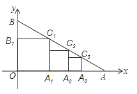
【题目】如图,在平面直角坐标系中,点A(![]() ,0),点B(0,1),作第一个正方形OA1C1B1且点A1在OA上,点B1在OB上,点C1在AB上;作第二个正方形A1A2C2B2且点A2在A1A上,点B2在A1C2上,点C2在AB上…,如此下去,则点Cn的纵坐标为________.
,0),点B(0,1),作第一个正方形OA1C1B1且点A1在OA上,点B1在OB上,点C1在AB上;作第二个正方形A1A2C2B2且点A2在A1A上,点B2在A1C2上,点C2在AB上…,如此下去,则点Cn的纵坐标为________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com