
【题目】已知![]() 中,
中,![]() 、
、![]() 分别为
分别为![]() 、
、![]() 上的点,且
上的点,且![]() ,
,![]() 交
交![]() 于
于![]() ,连
,连![]() 并延长交
并延长交![]() 于
于![]() .
.
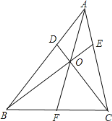
(1)当![]() 时,求
时,求![]() 的值;
的值;
(2)当![]() 时,求证:
时,求证:![]() ;
;
(3)当![]() ________时,
________时,![]() 为
为![]() 中点.
中点.
【答案】(1)![]() ;(2)详见解析;(3)
;(2)详见解析;(3)![]() .
.
【解析】
(1)连接DE交AF于K,根据平行线分线段成比例定理,即可证得DE∥BC,继而可得![]() ,根据比例的性质,即可求得
,根据比例的性质,即可求得![]() 的值;
的值;
(2)由n=1时,AD=BD,AE=CE,可得O是△ABC的重心,继而可得BF=CF;
(3)根据(1)的证明方法,即可求得答案.
(1)连接DE交AF于K.
∵![]() ,∴DE∥BC,∴
,∴DE∥BC,∴![]() ,∴设OK=a,则OF=3a,∴KF=4a,∴AK=2a,∴OA=AK+OK=3a,∴
,∴设OK=a,则OF=3a,∴KF=4a,∴AK=2a,∴OA=AK+OK=3a,∴![]() 1;
1;
(2)∵n=1时,AD=BD,AE=CE,∴O是△ABC的重心,∴AF是△ABC的中线,∴BF=CF;
(3)∵![]() ,∴DE∥BC,∴
,∴DE∥BC,∴![]() ,∴设OK=a,则OF=3a,∴KF=4a,∴AK=2a,∴OA=AK+OK=3a,∴
,∴设OK=a,则OF=3a,∴KF=4a,∴AK=2a,∴OA=AK+OK=3a,∴![]() 1,∴当n
1,∴当n![]() 时,O为AF中点.
时,O为AF中点.
故答案为:![]() .
.


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:初中数学 来源: 题型:
【题目】△ABC在平面直角坐标系中的位置如图所示,其中每个小正方形的边长为1个单位长度.
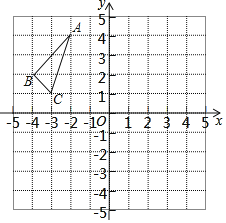
(1)△ABC关于y轴对称图形为△A1B1C1,画出△A1B1C1的图形.
(2)求△ABC的面积.
(3)若P点在x轴上,当BP+CP最小时,直接写出BP+CP最小值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】曲阜限制“三小车辆”出行后,为方便市民出行,准备为![]() 、
、![]() 、
、![]() 、
、![]() 四个村建一个公交车站
四个村建一个公交车站![]() .
.
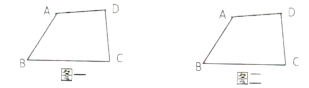
(1)请问:公交站![]() 建在何处才能使它到4个村的距离之和
建在何处才能使它到4个村的距离之和![]() 最小,请在图一中找出点
最小,请在图一中找出点![]() ;
;
(2)请问:公交站![]() 建在何处才能使它到道路
建在何处才能使它到道路![]() 、
、![]() 、
、![]() 的距离相等,请在图二中找出点
的距离相等,请在图二中找出点![]() 并加以说明.
并加以说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() 于点D,点E是直线AC上一动点,连接DE,过点D作
于点D,点E是直线AC上一动点,连接DE,过点D作![]() ,交直线BC于点F.
,交直线BC于点F.
![]() 探究发现:
探究发现:
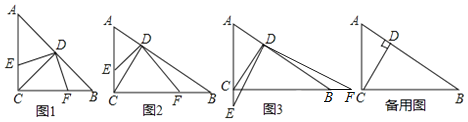
如图1,若![]() ,点E在线段AC上,则
,点E在线段AC上,则![]() ______;
______;
![]() 数学思考:
数学思考:
![]() 如图2,若点E在线段AC上,则
如图2,若点E在线段AC上,则![]() ______
______![]() 用含m,n的代数式表示
用含m,n的代数式表示![]() ;
;
![]() 当点E在直线AC上运动时,
当点E在直线AC上运动时,![]() 中的结论是否任然成立?请仅就图3的情形给出证明;
中的结论是否任然成立?请仅就图3的情形给出证明;
![]() 拓展应用:若
拓展应用:若![]() ,
,![]() ,
,![]() ,请直接写出CE的长.
,请直接写出CE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
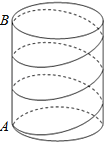
【题目】如图,圆柱底面半径为![]() cm,高为18cm,点A、B分别是圆柱两底面圆周上的点,且A、B在同一母线上,用一根棉线从A点顺着圆柱侧面绕3圈到B点,则这根棉线的长度最短为( )
cm,高为18cm,点A、B分别是圆柱两底面圆周上的点,且A、B在同一母线上,用一根棉线从A点顺着圆柱侧面绕3圈到B点,则这根棉线的长度最短为( )
A.24cmB.30cmC.2![]() cmD.4
cmD.4![]() cm
cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某种蔬菜每千克售价![]() (元)与销售月份
(元)与销售月份![]() 之间的关系如图1所示,每千克成本
之间的关系如图1所示,每千克成本![]() (元)与销售月份
(元)与销售月份![]() 之间的关系如图2所示,其中图1中的点在同一条线段上,图2中的点在同一条抛物线上,且抛物线的最低点的坐标为(6,1).
之间的关系如图2所示,其中图1中的点在同一条线段上,图2中的点在同一条抛物线上,且抛物线的最低点的坐标为(6,1).
(1)求出![]() 与
与![]() 之间满足的函数表达式,并直接写出
之间满足的函数表达式,并直接写出![]() 的取值范围;
的取值范围;
(2)求出![]() 与
与![]() 之间满足的函数表达式;
之间满足的函数表达式;
(3)设这种蔬菜每千克收益为![]() 元,试问在哪个月份出售这种蔬菜,
元,试问在哪个月份出售这种蔬菜,![]() 将取得最大值?并求出此最大值.(收益=售价-成本)
将取得最大值?并求出此最大值.(收益=售价-成本)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形OABC中,点O为原点,点A的坐标为(0,8),点C的坐标为(6,0).抛物线y=﹣![]() x2+bx+c经过点A、C,与AB交于点D.
x2+bx+c经过点A、C,与AB交于点D.
(1)求抛物线的函数解析式;
(2)点P为线段BC上一个动点(不与点C重合),点Q为线段AC上一个动点,AQ=CP,连接PQ,设CP=m,△CPQ的面积为S.
①求S关于m的函数表达式;
②当S最大时,在抛物线y=﹣![]() x2+bx+c的对称轴l上,若存在点F,使△DFQ为直角三角形,请直接写出所有符合条件的点F的坐标;若不存在,请说明理由.
x2+bx+c的对称轴l上,若存在点F,使△DFQ为直角三角形,请直接写出所有符合条件的点F的坐标;若不存在,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com