练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】曲阜限制“三小车辆”出行后，为方便市民出行，准备为、、、四个村建一个公交车站.

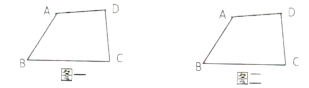
    （1）请问：公交站建在何处才能使它到4个村的距离之和最小，请在图一中找出点；

    （2）请问：公交站建在何处才能使它到道路、、的距离相等，请在图二中找出点并加以说明.

    【答案】（1）见解析；（2）见解析

    【解析】

    （1）公交站P是AC与BD的交点，要证这点到四点的距离最小，可以证明除这点以外的点到四点的距离大于这点到四点的距离；

    （2）公交站是∠ABC与∠DCB角平分线的交点，由角平分线性质定理可知，角平分线上的点到这个角两边的距离相等.

    解：（1）应建在AC，BD连线的交点P处，如图一，


    理由：如下图，若不建在P处，建在P1处，由三角形两边之和大于第三边可知，

    ，

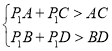    即P1A+P1C+P1B+P1D＞AC+BD，

    故结论成立应建在P处．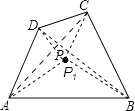

    即P1A+P1C+P1B+P1D＞AC+BD．
    故结论成立应建在P处．

    （2）应建在∠ABC与∠DCB角平分线的交点处，如图二，

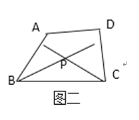
    理由：由角平分线性质定理可知，角平分线上的点到这个角两边的距离相等.

    所以点P道路、、的距离相等.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图1，在△ABC中，AB＝AC，∠BAC＝90°，D为AC边上一动点，且不与点A点C重合，连接BD并延长，在BD延长线上取一点E，使AE＝AB，连接CE．

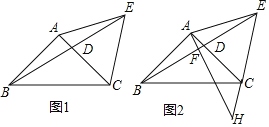
    （1）若∠AED＝20°，则∠DEC＝　 　度；

    （2）若∠AED＝a，试探索∠AED与∠AEC有怎样的数量关系？并证明你的猜想；

    （3）如图2，过点A作AF⊥BE于点F，AF的延长线与EC的延长线交于点H，求证：EH2+CH2＝2AE2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下列命题的逆命题成立的是（　　）．

    A.全等三角形的对应角相等

    B.若三角形的三边满足，则该三角形是直角三角形

    C.对顶角相等

    D.同位角互补，两直线平行

    查看答案和解析>>

    科目：初中数学 来源： 题型：

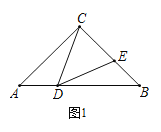
    【题目】如图，在等腰△ABC中，AC＝BC，D，E分别为AB，BC上一点，∠CDE＝∠A．

    （1）如图1，若BC＝BD，∠ACB＝90°，则∠DEC度数为_________°；

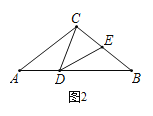
    （2）如图2，若BC＝BD，求证：CD＝DE；

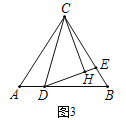
    （3）如图3，过点C作CH⊥DE，垂足为H，若CD＝BD，EH＝1，求DE－BE的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】定义：直线y=ax+b与直线y=bx+a互为“友好直线”．如：直线y=2x+1与直线y=x+2互为“友好直线”.

    （1）点M(m,2)在直线y=-x+4的“友好直线”上，则m=________；

    （2）直线y=4x+3上的一点M(m,n)又是它的“友好直线”上的点，求点M的坐标；

    （3）对于直线y=ax+b上的任意一点M(m,n),都有点N(2m,m-2n)在它的“友好直线”上，求直线y=ax+b的解析式．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知△ABC的周长是20，OB和OC分别平分∠ABC和∠ACB，OD⊥BC于点D，且OD=3，则△ABC的面积是（　　）

    A. 20 B. 25 C. 30 D. 35

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知中，、分别为、上的点，且，交于，连并延长交于．

    （1）当时，求的值；

    （2）当时，求证：；

    （3）当________时，为中点．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图①，已知直线y=-2x+4与x轴、y轴分别交于点A、C，以OA、OC为边在第一象限内作长方形OABC．

    （1）求点A、C的坐标；

    （2）将△ABC对折，使得点A的与点C重合，折痕交AB于点D，求直线CD的解析式（图②）；

    （3）在坐标平面内，是否存在点P（除点B外），使得△APC与△ABC全等？若存在，请直接写出所有符合条件的点P的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】[问题情境]

    已知矩形的面积为一定值1，当该矩形的一组邻边分别为多少时，它的周长最小？最小值是多少？

    [数学模型]

    设该矩形的一边长为x，周长为L，则L与x的函数表达式为　　　　．

    [探索研究]

    小彬借鉴以前研究函数的经验，先探索函数的图象性质．

    （1）结合问题情境，函数的自变量x的取值范围是　　　　，

    如表是y与x的几组对应值．

    x

    …

    1

    2

    3

    m

    …

    y

    …

    4

    3

    2

    2

    2

    3

    4

    …

    ①直接写出m的值；

    ②画出该函数图象，结合图象，得出当x=　　　　时，y有最小值，y的最小值为　　　　．

    [解决问题]

    （2）直接写出“问题情境”中问题的结论．

    查看答案和解析>>

    同步练习册答案