
【题目】如图,在△ABC中,AB=AC,∠ABM=∠CBN,MN=BN,则∠MBC的度数为_________°.
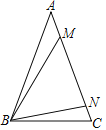
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A,B的坐标分别为(-1,0),(3,0),现同时将点A,B分别向上平移2个单位长度,再向右平移1个单位长度,得到A,B的对应点C,D,连接AC,BD,CD.
(1)直接写出点C,D的坐标,求出四边形ABDC的面积;
(2)在x轴上是否存在一点F,使得三角形DFC的面积是三角形DFB面积的2倍,若存在,请求出点F的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:如果一个数的平方等于![]() ,记为
,记为![]() ,这个数
,这个数![]() 叫做虚数单位。那么和我们所学的实数对应起来就叫做复数,表示为
叫做虚数单位。那么和我们所学的实数对应起来就叫做复数,表示为![]() (
(![]() 为实数),
为实数),![]() 叫这个复数的实部,
叫这个复数的实部, ![]() 叫做这个复数的虚部,它的加,减,乘法运算与整式的加,减,乘法运算类似。
叫做这个复数的虚部,它的加,减,乘法运算与整式的加,减,乘法运算类似。
例如计算: ![]()
(1)填空: ![]() =_________,
=_________, ![]() =____________.
=____________.
(2)填空:①![]() _________; ②
_________; ②![]() _________ 。
_________ 。
(3)若两个复数相等,则它们的实部和虚部必须分别相等,完成下列问题:已知, ![]() ,(
,( ![]() 为实数),求
为实数),求![]() 的值。
的值。
(4)试一试:请利用以前学习的有关知识将![]() 化简成
化简成![]() 的形式。
的形式。
(5)解方程:x2 - 2x +4 = 0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题的逆命题成立的是( ).
A.全等三角形的对应角相等
B.若三角形的三边满足![]() ,则该三角形是直角三角形
,则该三角形是直角三角形
C.对顶角相等
D.同位角互补,两直线平行
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于点
的图象交于点![]() ,点
,点![]() 在第一象限,
在第一象限,![]() 轴于点
轴于点![]() ,
,![]() 轴于点
轴于点![]() .一次函数的图象分别交
.一次函数的图象分别交![]() 轴、
轴、![]() 轴于点
轴于点![]() 、
、![]() ,且
,且![]() ,
,![]() ,
,![]() .
.
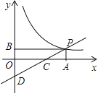
(1)求点![]() 的坐标;
的坐标;
(2)求一次函数与反比例函数的解析式:
(3)根据图象写出当![]() 时,一次函数的值小于反比例函数的值的
时,一次函数的值小于反比例函数的值的![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰△ABC中,AC=BC,D,E分别为AB,BC上一点,∠CDE=∠A.
(1)如图1,若BC=BD,∠ACB=90°,则∠DEC度数为_________°;
(2)如图2,若BC=BD,求证:CD=DE;
(3)如图3,过点C作CH⊥DE,垂足为H,若CD=BD,EH=1,求DE-BE的值.
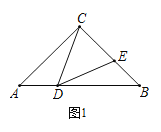
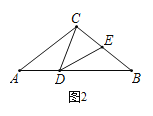
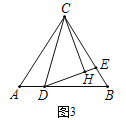
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:直线y=ax+b与直线y=bx+a互为“友好直线”.如:直线y=2x+1与直线y=x+2互为“友好直线”.
(1)点M(m,2)在直线y=-x+4的“友好直线”上,则m=________;
(2)直线y=4x+3上的一点M(m,n)又是它的“友好直线”上的点,求点M的坐标;
(3)对于直线y=ax+b上的任意一点M(m,n),都有点N(2m,m-2n)在它的“友好直线”上,求直线y=ax+b的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图,正方形ABCD中,点E,F分别在边BC,CD上,∠EAF=45°,延长CD到点G,使DG=BE,连结EF,AG.求证:EF=FG.
(2)如图,等腰直角三角形ABC中,∠BAC=90°,AB=AC,点M,N在边BC上,且∠MAN=45°,若BM=1,CN=3,求MN的长.
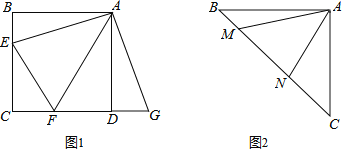
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com