
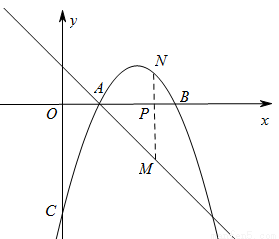
已知抛物线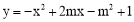 与x轴交点为A、B(点B在点A的右侧),与y轴交于点C.
与x轴交点为A、B(点B在点A的右侧),与y轴交于点C.
(1)试用含m的代数式表示A、B两点的坐标;
(2)当点B在原点的右侧,点C在原点的下方时,若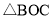 是等腰三角形,求抛物线的解析式;
是等腰三角形,求抛物线的解析式;
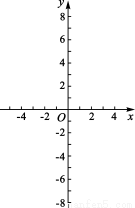
(3)已知一次函数 ,点P(n,0)是x轴上一个动点,在(2)的条件下,过点P作垂直于x轴的直线交这个一次函数的图象于点M,交抛物线
,点P(n,0)是x轴上一个动点,在(2)的条件下,过点P作垂直于x轴的直线交这个一次函数的图象于点M,交抛物线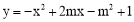 于点N,若只有当
于点N,若只有当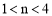 时,点M位于点N的下方,求这个一次函数的解析式.
时,点M位于点N的下方,求这个一次函数的解析式.
(1)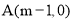 ;(2)
;(2)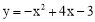 ;(3)
;(3)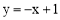 .
.
【解析】
试题分析:(1)根据点在曲线上点的坐标满足方程的关系,令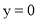 ,解出即可求得用含m的代数式表示的A、B两点坐标.
,解出即可求得用含m的代数式表示的A、B两点坐标.
(2)根据等腰三角形的性质,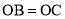 ,列式求出m的值即可求得抛物线的解析式.
,列式求出m的值即可求得抛物线的解析式.
(3)依题意并结合图象可知,一次函数的图象与二次函数的图象交点的横坐标分别为1和4,由此可得交点坐标,应用待定系数法,将交点坐标分别代入一次函数解析式即可求解.
试题解析:(1)令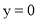 ,有
,有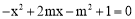 .
.
∴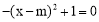 . ∴
. ∴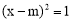 .
.
∴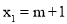 ,
,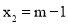 .
.
∵点B在点A的右侧,∴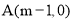 ,
,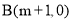 .
.
(2)∵点B在原点的右侧且在点A的右侧,点C在原点的下方,抛物线开口向下,
∴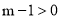 .∴
.∴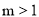 .∴
.∴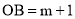 .
.
令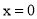 ,有
,有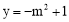 .∴
.∴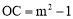 .
.
∵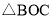 是等腰三角形,且∠BOC =90°,
是等腰三角形,且∠BOC =90°,
∴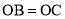 ,即
,即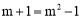 .
.
∴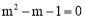 ,解得
,解得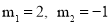 (舍去).
(舍去).
∴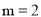 .
.
∴抛物线的解析式为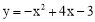 .
.
(3)依题意并结合图象可知,一次函数的图象与二次函数的图象交点的横坐标分别为1和4,
由此可得交点坐标为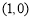 和
和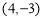 .
.
将交点坐标分别代入一次函数解析式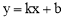 中,
中,
得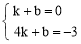 , 解得
, 解得 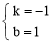 .
.
∴一次函数的解析式为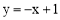 .
.
考点:1.二次函数综合题;2.动点问题;3.待定系数法的应用;4.曲线上点的坐标与方程的关系;5.等腰三角形的性质;6.数形结合思想的应用.


 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案科目:初中数学 来源:2013-2014学年四川省乐山市夹江县九年级毕业会考适应性考试数学试卷(解析版) 题型:解答题
有一人患了流感,经过两轮传染后共有64人患了流感.
(1)求每轮传染中平均一个人传染了几个人?
(2)如果不及时控制,第三轮将又有多少人被传染?
查看答案和解析>>
科目:初中数学 来源:2013-2014学年吉林省长春市朝阳区中考一模数学试卷(解析版) 题型:选择题
2014年3月21日上午,我国新型导弹驱逐舰昆明舰举行入列仪式,正式加入人民海军战斗序列.昆明舰采用柴燃交替动力,配备2台QC208燃气轮机,单台功率37500马力.数据37500用科学记数表示为( )
A.3.75×104 B.37.5×103 C.0.375×105 D.3.75×103
查看答案和解析>>
科目:初中数学 来源:2013-2014学年北京市顺义区中考二模数学试卷(解析版) 题型:选择题
某中学九(1)班6个同学在课间体育活动时进行1分钟跳绳比赛,跳绳个数如下:
126,144,134,118,126,152.这组数据中,众数和中位数分别是( )
A.126,126 B.130,134 C.126,130 D.118,152
查看答案和解析>>
科目:初中数学 来源:2013-2014学年北京市顺义区中考一模数学试卷(解析版) 题型:解答题
列方程或方程组解应用题:
重量相同的甲、乙两种商品,分别价值900元和1 500元,已知甲种商品每千克的价值比乙种商品每千克的价值少100元,分别求甲、乙两种商品每千克的价值.
查看答案和解析>>
科目:初中数学 来源:2013-2014学年北京市顺义区中考一模数学试卷(解析版) 题型:填空题
已知小聪的身高为1.8米,在太阳光下的地面影长为2.4米,若此时测得一旗杆在同一地面的影长为20米,则旗杆高应为 .
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(黑龙江龙东卷)数学(解析版) 题型:解答题
如图,方格纸中每个小正方形的边长都是1个单位长度,Rt△ABC的三个顶点A(﹣2,2),B(0,5),C(0,2).
(1)将△ABC以点C为旋转中心旋转180°,得到△A1B1C,请画出△A1B1C的图形.
(2)平移△ABC,使点A的对应点A2坐标为(﹣2,﹣6),请画出平移后对应的△A2B2C2的图形.
(3)若将△A1B1C绕某一点旋转可得到△A2B2C2,请直接写出旋转中心的坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com