
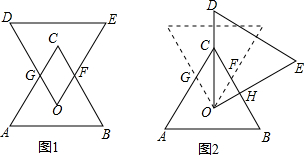
 如图(1),有两个全等的正三角形ABC和ODE,点O、C分别为△ABC、△DEO的重心;固定点O,将△ODE顺时针旋转,使得OD经过点C,如图(2),则图(2)中四边形OGCF与△OCH面积的比为
如图(1),有两个全等的正三角形ABC和ODE,点O、C分别为△ABC、△DEO的重心;固定点O,将△ODE顺时针旋转,使得OD经过点C,如图(2),则图(2)中四边形OGCF与△OCH面积的比为 解:设正三角形的边长是x,则高长是
解:设正三角形的边长是x,则高长是
| ||
| 2 |
| 2 |
| 3 |
| ||
| 2 |
| ||
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| ||
| 3 |
| ||
| 18 |
| 2 |
| 3 |
| ||
| 2 |
| ||
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 3 |
| 1 |
| 2 |
| ||
| 3 |
| ||
| 2 |
| ||
| 24 |
| ||
| 18 |
| ||
| 24 |


 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案科目:初中数学 来源: 题型:
 已知在平面直角坐标系中,点O为坐标原点,过O的直线OM经过点A(6,6),过A作正方形ABCD,在直线OA上有一点E,过E作正方形EFGH,已知直线OC经过点G,且正方形ABCD的边长为2,正方形EFGH的边长为3,则点F的坐标为
已知在平面直角坐标系中,点O为坐标原点,过O的直线OM经过点A(6,6),过A作正方形ABCD,在直线OA上有一点E,过E作正方形EFGH,已知直线OC经过点G,且正方形ABCD的边长为2,正方形EFGH的边长为3,则点F的坐标为查看答案和解析>>
科目:初中数学 来源: 题型:
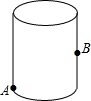 没有上盖的圆柱盒高为10cm,底面周长为32cm,点A距离下底面3cm.一只位于圆柱盒外表面点A处的蚂蚁想爬到盒内表面对侧中点B处.则蚂蚁需要爬行的最短路程的长为
没有上盖的圆柱盒高为10cm,底面周长为32cm,点A距离下底面3cm.一只位于圆柱盒外表面点A处的蚂蚁想爬到盒内表面对侧中点B处.则蚂蚁需要爬行的最短路程的长为查看答案和解析>>
科目:初中数学 来源: 题型:
| ( ) |
| ( ) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com