
| 波长(m) | 300 | 500 | 600 | 1000 | 1500 |
| 频率(kHz) | 1000 | 600 | 500 | 300 | 200 |
分析 (1)根据波长和频率的乘积是定值确定二者的关系并求得其表达式;
(2)根据其增减性和频率的取值范围确定波长的取值范围即可.
解答 解:(1)观察表格发现fλ=300×1000=500×600=600×500=1000×300=1500×200=30000,
所以可判断频率f是波长λ的反比例函数,其表达式为f=$\frac{30000}{λ}$;
故答案为:反比例,f=$\frac{30000}{λ}$;
(2)当f=400kHz时,λ=$\frac{30000}{400}$=750,
所以当频率f不超过400kHz时,波长λ(米)的取值范围是λ≥750.
点评 本题考查了反比例函数的知识,解题的关键是从实际问题中整理出反比例函数模型,难度不大.


科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | -1 | C. | $\frac{1}{49}$ | D. | -$\frac{1}{49}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
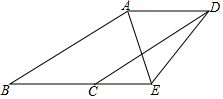 已知如图,∠ABC=∠ADC,AB∥CD,AE平分∠BAD,当∠ADC:∠CDE=3:2,且∠AED=60°时,求∠BED的度数为$\frac{960}{7}$度.
已知如图,∠ABC=∠ADC,AB∥CD,AE平分∠BAD,当∠ADC:∠CDE=3:2,且∠AED=60°时,求∠BED的度数为$\frac{960}{7}$度.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
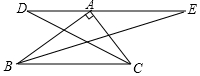 如图,在△ABC中,∠BAC=90°,AC=6,BC=10,过点A的直线DE∥BC,∠ABC与∠ACB的平分线分别交DE于E,D,求DE的长.
如图,在△ABC中,∠BAC=90°,AC=6,BC=10,过点A的直线DE∥BC,∠ABC与∠ACB的平分线分别交DE于E,D,求DE的长.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com