
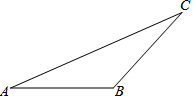
 如图,已知△ABC中,∠B>90°,请用尺规作出AB边的高线CD(请留作图痕迹,不写作法)
如图,已知△ABC中,∠B>90°,请用尺规作出AB边的高线CD(请留作图痕迹,不写作法) 科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
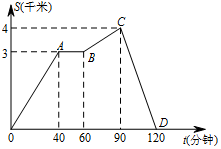 为了提高身体素质,小明假期为自己制定了慢跑锻炼计划,某日小明从省体育场出发沿长安路慢跑,已知他离省体育场的距离s( km)与时间t(h)之间的关系如图所示,根据图象回答下列问题:
为了提高身体素质,小明假期为自己制定了慢跑锻炼计划,某日小明从省体育场出发沿长安路慢跑,已知他离省体育场的距离s( km)与时间t(h)之间的关系如图所示,根据图象回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
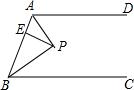 如图,AD∥BC,∠ABC的角平分线BP与∠BAD的角平分线AP相交于点P,作PE⊥AB于点E,若PE=3,则两平行线AD与BC间的距离为6.
如图,AD∥BC,∠ABC的角平分线BP与∠BAD的角平分线AP相交于点P,作PE⊥AB于点E,若PE=3,则两平行线AD与BC间的距离为6.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 波长(m) | 300 | 500 | 600 | 1000 | 1500 |
| 频率(kHz) | 1000 | 600 | 500 | 300 | 200 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com