
【题目】如图,![]() ,
,![]() ,
,![]() .求
.求![]() 的度数.
的度数.

请将求![]() 的度数的过程及理由填写出来.
的度数的过程及理由填写出来.
解:∵![]() (已知),
(已知),
∴![]() (______________________).
(______________________).
又∵![]() (已知),
(已知),
∴![]() (______________________).
(______________________).
∴![]() __________(______________________).
__________(______________________).
∴![]() __________
__________![]() (______________________).
(______________________).
又∵![]() (已知),
(已知),
∴![]() _________.
_________.
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
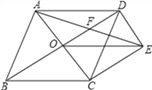
【题目】如图,菱形ABCD的对角线AC、BD相交于点O,过点D作DE∥AC且DE=![]() AC,连接AE交OD于点F,连接CE、OE.
AC,连接AE交OD于点F,连接CE、OE.
(1)求证:OE=CD;
(2)若菱形ABCD的边长为2,∠ABC=60°,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校为了增强学生体质,决定开设以下体育课外活动项目:A.篮球 B.乒乓球C.羽毛球 D.足球,为了解学生最喜欢哪一种活动项目,随机抽取了部分学生进行调查,并将调查结果绘制成了两幅不完整的统计图,

请回答下列问题:
(1)这次被调查的学生共有多少人?
(2)请你将条形统计图(2)补充完整;
(3)在平时的乒乓球项目训练中,甲、乙、丙、丁四人表现优秀,现决定从这四名同学中任选两名参加乒乓球比赛,求恰好选中甲、乙两位同学的概率(用树状图或列表法解答)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】分解因式x2-4y2-2x+4y,细心观察这个式子就会发现,前两项符合平方差公式,后两项可提取公因式,前后两部分分别分解因式后会产生公因式,然后提取公因式就可以完成整个式子的分解因式,过程为:x2-4y2-2x+4y=(x+2y)(x-2y)-2(x-2y)=(x-2y)(x+2y-2).这种分解因式的方法叫分组分解法,利用这种方法解决下列问题:
(1)分解因式:a2-4a-b2+4;
(2)若△ABC三边a、b、c满足a2-ab-ac+bc=0,试判断△ABC的形状.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学组织学生春游,原计划租用45座客车若干辆,但有15人没有座位;若租用同样数量的60座客车,则多出一辆车,且其余客车恰好坐满,已知45座客车每日每辆租金为220元,60座客车每日每辆租金为300元.试问:
(1)春游学生共多少人,原计划租45座客车多少辆?
(2)若租用同一种车,要使每位同学都有座位,怎样租车更合算.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AC⊥x轴于点A,点B在y轴的正半轴上,∠ABC=60°,AB=4,BC=![]() ,点D为AC与反比例函数
,点D为AC与反比例函数![]() 的图象的交点.若直线BD将△ABC的面积分成1:2的两部分,则k的值为______.
的图象的交点.若直线BD将△ABC的面积分成1:2的两部分,则k的值为______.

查看答案和解析>>
科目:初中数学 来源: 题型:
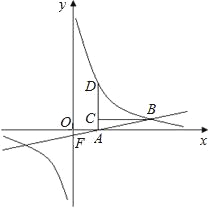
【题目】如图,点D在双曲线上,AD垂直x轴,垂足为A,点C在AD上,CB平行于x轴交双曲线于点B,直线AB与y轴交于点F,已知AC:AD=1:3,点C的坐标为(3,2).
(1)求该双曲线的解析式;
(2)求△OFA的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料,解答后面的问题:
材料:求代数式x2-2x+5的最小值.
小明同学的解答过程:x2-2x+5=x2-2x+1-1+5=(x-1)2+4
我们把这种解决问题的方法叫做“配方法”.
(1)请按照小明的解题思路,写出完整的解答过程;
(2)请运用“配方法”解决问题:
①若x2+y2-6x+10y+34=0,求y-x的立方根;
②分解因式:4x4+1.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,按照
,按照![]() 的顺序,分别将这六个点的横、纵坐标依次循环排列下去,形成一组数1,1,-1,2,2,3,-2,4,3,5,-3,6,1,1,-1,2,…,第一个数记为
的顺序,分别将这六个点的横、纵坐标依次循环排列下去,形成一组数1,1,-1,2,2,3,-2,4,3,5,-3,6,1,1,-1,2,…,第一个数记为![]() ,第二个数记为
,第二个数记为![]() ,…,第
,…,第![]() 个数记为
个数记为![]() (
(![]() 为正整数),那么
为正整数),那么![]() 和
和![]() 的值分别为( )
的值分别为( )

A. 0,3B. 0,2C. 6,3D. 6,2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com